题目内容
小于88的两位正整数,它的个位数字比十位数字大4,这样的两位数有_________个.
 5
【解析】设十位数字为x,则个位数字为x+4
依题意得10x+x+4<88
得x<
又∵x应为正整数,且大于0;并且0≤个位数字≤9,因而5≤x+4≤9
∴1≤x≤5,故这样的两位数有5个.
故答案:5.
5
【解析】设十位数字为x,则个位数字为x+4
依题意得10x+x+4<88
得x<
又∵x应为正整数,且大于0;并且0≤个位数字≤9,因而5≤x+4≤9
∴1≤x≤5,故这样的两位数有5个.
故答案:5.
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
把分式 中的m和n都扩大4倍,那么分式的值( )
中的m和n都扩大4倍,那么分式的值( )
A. 也扩大4倍 B. 扩大为原来的4倍 C. 不变 D. 缩小为原来的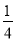
 C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C.
C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C. 如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )

A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF
 D
【解析】∵AB∥CD,
∴∠A=∠C,
又∵AE=CF,
∴(1)添加“AB=CD”,可由“SAS”判定△ABE≌△CDF;
(2)添加“BE∥DF”可得∠FEB=∠EFD,进一步可得∠AEB=∠CFD,从而可由“ASA”判定△ABE≌△CDF;
(3)添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF;
(4)添加“BE=DF”不能判定△ABE≌...
D
【解析】∵AB∥CD,
∴∠A=∠C,
又∵AE=CF,
∴(1)添加“AB=CD”,可由“SAS”判定△ABE≌△CDF;
(2)添加“BE∥DF”可得∠FEB=∠EFD,进一步可得∠AEB=∠CFD,从而可由“ASA”判定△ABE≌△CDF;
(3)添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF;
(4)添加“BE=DF”不能判定△ABE≌... 甲、乙原有存款800元和1800元,从本月开始,甲每月存400元,乙每月存200元.如果设两人存款时间为x月.甲存款额是y1元,乙存款额是y2元.
(1)试写出y1与x及y2与x之间的函数关系式;
(2)到第几个月时,甲存款额能超过乙存款额?
 详见解析
【解析】
试题分析:(1)根据存款数=原有存款+又存入的钱数,列式即可;
(2)列出一元一次不等式,然后求解即可.
【解析】
(1)根据题意,甲:y1=400x+800,
乙:y2=200x+1800;
(2)根据题意,400x+800>200x+1800,
解得x>5,
所以,从第6个月开始,甲存款额能超过乙存款额.
详见解析
【解析】
试题分析:(1)根据存款数=原有存款+又存入的钱数,列式即可;
(2)列出一元一次不等式,然后求解即可.
【解析】
(1)根据题意,甲:y1=400x+800,
乙:y2=200x+1800;
(2)根据题意,400x+800>200x+1800,
解得x>5,
所以,从第6个月开始,甲存款额能超过乙存款额. 直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
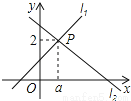
 x≥1
【解析】
试题分析:首先把P(a,2)坐标代入直线y=x+1,求出a的值,从而得到P点坐标,再根据函数图象可得答案.
【解析】
将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1.
x≥1
【解析】
试题分析:首先把P(a,2)坐标代入直线y=x+1,求出a的值,从而得到P点坐标,再根据函数图象可得答案.
【解析】
将点P(a,2)坐标代入直线y=x+1,得a=1,
从图中直接看出,当x≥1时,x+1≥mx+n,
故答案为:x≥1. 不等式组 的最小整数解为( )
的最小整数解为( )
A. ﹣1 B. 0 C. 1 D. 4
 B
【解析】解3x﹣4≤8,得:x≤4,
则不等式组的解集是:﹣<x≤4.
则最小的整数解是:0.
故选B.
B
【解析】解3x﹣4≤8,得:x≤4,
则不等式组的解集是:﹣<x≤4.
则最小的整数解是:0.
故选B. 在数轴上表示不等式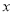 ≥-2的解集,正确的是( )
≥-2的解集,正确的是( )
A. 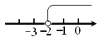 B.
B. 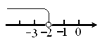 C.
C. 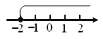 D.
D. 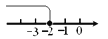
 C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C.
C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为______.
 6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
故答案为:6.
6
【解析】∵多边形的外角和是360度,多边形的内角和是外角和的2倍,
则内角和是720度,
720÷180+2=6,
∴这个多边形是六边形,
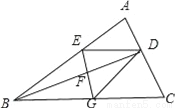
故答案为:6. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2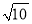 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
 (1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:...
(1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:... 
