题目内容
一次函数y=﹣3x+12中x_________ 时，y＜0．
＞4
【解析】根据题意得：﹣3x+12＜0，
解得：x＞4．
故答案为：＞4；
练习册系列答案
相关题目
计算：
＝_______
【解析】试题分析：原式＝＝＝＝．
故答案为： ． 如图，△ABC和△AED中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD、CE，求证：BD=EC。
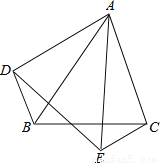
证明见解析
【解析】试题分析：
由∠BAC=∠DAE易得∠BAD=∠EAC，结合AB=AE，AC=AD，即可由“SAS”证得：△BAD≌△EAC，从而可得：BD=EC.
试题解析：
∵∠DAE=∠BAC，
∴∠DAE-∠BAE=∠EAC-∠BAE，
∴∠BAD=∠EAC，
在△BAD和△EAC中，
∴△BAD≌△EAC（SAS），
∴BD=EC... 小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3（2x-100）＜1000，则下列何者可能是小美告诉小明的内容？（ ）
A. 买两件等值的商品可减100元，再打3折，最后不到1000元
B. 买两件等值的商品可减100元，再打7折，最后不到1000元
C. 买两件等值的商品可打3折，再减100元，最后不到1000元
D. 买两件等值的商品可打7折，再减100元，最后不到1000元
A
【解析】【解析】
由关系式可知：
0.3（2x﹣100）＜1000，
由2x﹣100，得出两件商品减100元，以及由0.3（2x﹣100）得出买两件打3折，
故可以理解为：买两件等值的商品可减100元，再打3折，最后不到1000元．
故选A． 已知不等式组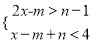
的解集为﹣1＜x＜1，则（m+n）2014的值等于多少？
1
【解析】【试题分析】解不等式解不等式2x﹣m＞n﹣1得x＞，由不等式组的解集为﹣1＜x＜1可得=﹣1，从而知m+n的值，代入即可．
【试题解析】
解不等式2x﹣m＞n﹣1，得：x＞，
∵不等式组的解集为﹣1＜x＜1，
∴=﹣1，
∴m+n=﹣1，
则（m+n）2014=（﹣1）2014=1． 不等式组﹣1＜x＜4的整数解有_________个．
4
【解析】在﹣1＜x＜4范围内的整数只有0，1，2，3，
所以等式﹣1＜x＜4的整数解有4个，
故答案为4． 不等式组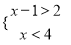
的解集是（ ）
A. x＜3 B. 3＜x＜4 C. x＜4 D. 无解
B
【解析】解不等式x﹣1＞2，得：x＞3，
∴不等式组的解集为：3＜x＜4，
故选：B． 如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为__．
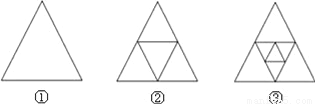
4n﹣3
【解析】试题解析：第①是1个三角形，1=4×1-3；
第②是5个三角形，5=4×2-3；
第③是9个三角形，9=4×3-3；
∴第n个图形中共有三角形的个数是4n-3 在下列条件中，能够判定一个四边形是平行四边形的是（ ）
A. 一组对边平行，另一组对边相等
B. 一组对边相等，一组对角相等
C. 一组对边平行，一条对角线平分另一条对角线
D. 一组对边相等，一条对角线平分另一条对角线
C
【解析】A、错误．这个四边形有可能是等腰梯形．
B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．
D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
故选C．