题目内容
不等式组﹣1<x﹣5<11的解集是_________.
 4<x<16
【解析】不等式每个部分都加5得,4<x<16.
故答案为:4<x<16.
4<x<16
【解析】不等式每个部分都加5得,4<x<16.
故答案为:4<x<16.
练习册系列答案
相关题目
下列各式与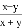 相等的是( )
相等的是( )
A. 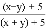 B.
B. 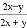
C. 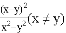 D.
D. 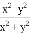
 C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C.
C
【解析】试题分析:因为不能约分,所以,所以A错误;因为不能约分,所以,所以B错误;因为,所以C正确;因为不能约分,所以,所以D错误;故选:C. 如图,已知AC与BD相交于点O,OA=OC,OB=OD,则图中有多少对三角形全等( )
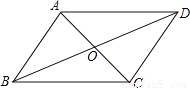
A. 1 B. 2 C. 3 D. 4
 D
【解析】∵AC与BD相交于点O,
∴∠AOD=∠COB,∠AOB=∠COD,
又∵OA=OC,OB=OD,
∴△AOD≌△COB,△AOB≌△COD,
∴AD=CB,AB=CD,
又∵AC=CA,BD=DB,
∴△ACD≌△CAB,△ABD≌△CDB,
即图中共有4对全等三角形.
故选D.
D
【解析】∵AC与BD相交于点O,
∴∠AOD=∠COB,∠AOB=∠COD,
又∵OA=OC,OB=OD,
∴△AOD≌△COB,△AOB≌△COD,
∴AD=CB,AB=CD,
又∵AC=CA,BD=DB,
∴△ACD≌△CAB,△ABD≌△CDB,
即图中共有4对全等三角形.
故选D. 在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
 (1)每台电脑0.5万元,每台电子白板1.5万元;(2)方案3最省钱,即购买电脑17台,电子白板13台最省
【解析】试题分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;
(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用...
(1)每台电脑0.5万元,每台电子白板1.5万元;(2)方案3最省钱,即购买电脑17台,电子白板13台最省
【解析】试题分析:(1)先设每台电脑x万元,每台电子白板y万元,根据购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元列出方程组,求出x,y的值即可;
(2)先设需购进电脑a台,则购进电子白板(30﹣a)台,根据需购进电脑和电子白板共30台,总费用... 解不等式,并把解集在数轴上表示出来:
(1)5x﹣6≤2(x+3);
(2)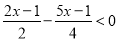
 (1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
...
(1)x≤4; (2)x>﹣1,
【解析】【试题分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
【试题解析】(1)去括号,得:5x﹣6≤2x+6,
移项,得:5x﹣2x≤6+6,
合并同类项,得:3x≤12,
系数化为1,得:x≤4,
... 已知三角形的两边为3和4,则第三边a的取值范围是________.
 1<a<7
【解析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,得4-3<a<4+3,即1<a<7.
故答案为:1<a<7.
1<a<7
【解析】根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,得4-3<a<4+3,即1<a<7.
故答案为:1<a<7. 如图,当y<0时,自变量x的范围是( )
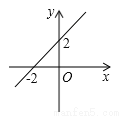
A.x<-2 B.x>-2 C.x<2 D.x>2
 A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
故选A.
A.
【解析】
试题解析:由图象可得,一次函数的图象与x轴的交点为(-2,0),当y<0时,x<-2.
故选A. 如图,在?ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是_______.
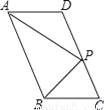
 24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD...
24
【解析】试题分析:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= (∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD... 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
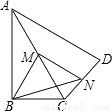
 (1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=...
(1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=... 
