题目内容
解不等式组：
（1）
；
（2）
．
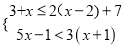（1）0＜x≤4；（2）0≤x＜2．
【解析】【试题分析】（1）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集；
（2）分别求出每一个不等式的解集，根据口诀：大小小大中间找即可确定不等式组的解集．
【试题解析】
（1）解不等式5x﹣6≤2（x+3），得：x≤4，
解不等式，得：x＞0，
∴不等式组的解集为0＜x≤4；
（2）解不...
练习册系列答案
阅读快车系列答案
相关题目
________.
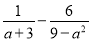【解析】试题分析：
＝
＝
＝
＝．
故答案为： ． 如图，点B、D、E、C在一条直线上，△ABD≌△ACE，AB和AC，AD和AE是对应边，除△ABD≌△ACE外，图中还有其他全等三角形吗？若有，请写出来，并证明你的结论。
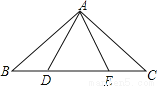
有，△ABE≌△ACD
【解析】试题分析：
由△ABD≌△ACE可得：AB=AC，BD=CE，∠B=∠C，从而易得BE=CD，这样由“SAS”即可证得△ABE和△ACD.
试题解析：
有，△ABE≌△ACD；理由如下：
∵△ABD≌△ACE，
∴AB=AC，BD=CE，∠B=∠C，
∴BE=CD，
在△ABE和△ACD中，
，
∴△ABE... 某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分，娜娜得分要超过90分，设她答对了n道题，则根据题意可列不等式 ．
10n﹣5（20﹣n）＞90
【解析】根据答对题的得分：10n；答错题的得分：﹣5（20﹣n），得出不等关系：得分要超过90分．
【解析】
根据题意，得10n﹣5（20﹣n）＞90．
故答案为：10n﹣5（20﹣n）＞90． 甲、乙原有存款800元和1800元，从本月开始，甲每月存400元，乙每月存200元．如果设两人存款时间为x月．甲存款额是y1元，乙存款额是y2元．
（1）试写出y1与x及y2与x之间的函数关系式；
（2）到第几个月时，甲存款额能超过乙存款额？
详见解析
【解析】
试题分析：（1）根据存款数=原有存款+又存入的钱数，列式即可；
（2）列出一元一次不等式，然后求解即可．
【解析】
（1）根据题意，甲：y1=400x+800，
乙：y2=200x+1800；
（2）根据题意，400x+800＞200x+1800，
解得x＞5，
所以，从第6个月开始，甲存款额能超过乙存款额． 若不等式组
有解，则a的取值范围是__________________.
a≤2
【解析】∵x≤2且x≥a，要使2者有公共部分,必须满足：a≤2.
∴a的取值范围是a≤2. 不等式组
的最小整数解为（ ）
A. ﹣1 B. 0 C. 1 D. 4
B
【解析】解3x﹣4≤8，得：x≤4，
则不等式组的解集是：﹣＜x≤4．
则最小的整数解是：0．
故选B． 如图，在?ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
（1）求证：AB=CF；
（2）连接DE，若AD=2AB，求证：DE⊥AF．
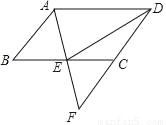
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由在?ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB∥DF， ∴∠ABE=∠FCE， ∵E为BC中点， ∴BE=C... 如图，在?ABCD中，AB＝6，BC＝8，∠BCD的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于( )
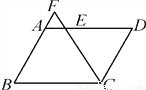
A. 2 B. 3 C. 4 D. 6
C
【解析】试题分析：由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．∵四边形ABCD是平行四边形， ∴AB∥CD，AD=BC=8，CD=AB=6，
∴∠F=∠DCF，∵∠C平分线为CF，∴∠FCB=∠DCF，∴∠F=∠FCB， ∴BF=BC=8，
同理：DE=CD=6， ∴A...