在下列条件中,不能说明△ABC≌△A’B’C’的是( )
A. ∠A=∠A’,∠C=∠C’,AC=A’C’ B. ∠A=∠A’,AB=A’B’,BC=B’C’
C. ∠B=∠B’,∠C=∠C’,AB=A’B’ D. AB=A’B’, BC=B’ C’AC=A’C’
 B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB...
B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB... 在下列说法中,正确的有( )个.
①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角,一边对应相等的两个三角形全等;④两边,一角对应相等的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
 B
【解析】①三角对应相等的两个三角形不一定全等,错误;
②三边对应相等的两个三角形全等,正确;
③两个角和其中一角的对边对应相等的两个三角形全等,正确;
④两条边和其中一边的对角对应相等的两个三角形不一定全等,错误;
故选:B
B
【解析】①三角对应相等的两个三角形不一定全等,错误;
②三边对应相等的两个三角形全等,正确;
③两个角和其中一角的对边对应相等的两个三角形全等,正确;
④两条边和其中一边的对角对应相等的两个三角形不一定全等,错误;
故选:B 下列说法正确的是( )
A. 两个周长相等的长方形全等 B. 两个周长相等的三角形全等
C. 两个面积相等的长方形全等 D. 两个周长相等的圆全等
 D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D.
D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D. 使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
 D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...
D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错... 如图,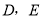 分别为
分别为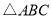 的
的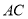 ,
,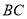 边的中点,将此三角形沿
边的中点,将此三角形沿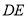 折叠,使点
折叠,使点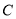 落在
落在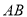 边上的点
边上的点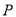 处.若
处.若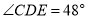 ,则
,则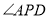 等于( )
等于( )
A.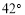 B.
B.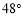 C.
C.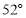 D.
D.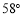
 B
【解析】
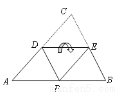
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=.
B
【解析】
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=. 如图,△ABC≌△CDA,且AD=CB,下列结论错误的是( )
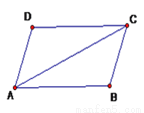
A. ∠B=∠D B. ∠CAB=∠ACD C. BC=CD D. AC=CA
 C
【解析】∵△ABC≌△CDA,
∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A. B.D正确,不符合题意,
BC不一定等于CD,C错误,符合题意,
故选:C.
C
【解析】∵△ABC≌△CDA,
∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A. B.D正确,不符合题意,
BC不一定等于CD,C错误,符合题意,
故选:C. 已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
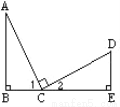
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△CED D. ∠1=∠2
 D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=...
D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=... 如图,AC=AD,BC=BD,则有( )
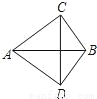
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
 A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.
A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A. 如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
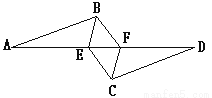
A. 1对 B. 2对 C. 3对 D. 4对
 C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)...
C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)... 已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
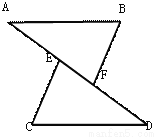
A. SSS B. SAS C. ASA D. HL
 D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.
D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.