题目内容
已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
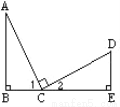
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△CED D. ∠1=∠2
D
【解析】∵AC⊥CD，
∴∠1+∠2=90°，
∵∠B=90°，
∴∠1+∠A=90°，
∴∠A=∠2，
在△ABC和△CED中，
，
∴△ABC≌△CED(AAS)，
故B、C选项正确；
∵∠2+∠D=90°，
∴∠A+∠D=90°，
故A选项正确；
∵AC⊥CD，
∴∠ACD=90°，
∠1+∠2=...
练习册系列答案
出彩同步大试卷系列答案
相关题目
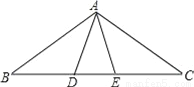
如图所示，在△ABC中，AB=AC，点D、E在BC边上，∠ABD=∠DAE=∠EAC=36°，则图中共有等腰三角形的个数是__．
6
【解析】【解析】
∵AB=AC，∠ABD=36°，即△ABC是等腰三角形，∴∠C=∠B=36°，∴∠BAC=108°．
∵∠DAE=∠EAC=36°，∴∠BAD=36°，∴∠BAD=∠B=36°，∠EAC=∠C=36°，∴△ABD，△ACE是等腰三角形，∴∠ADE=∠AED=∠DAC=∠BAE=72°，∴△ADE，△ABE，△ACD是等腰三角形．
故答案为：6．
... 因式分解: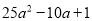 
=______________
【解析】根据完全平方公式进行因式分解为： =.
故答案为： . 如图所示，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，且BD=CD，那么BE与CF相等吗？为什么？
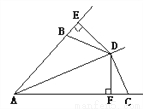
见解析
【解析】试题分析：首先由角平分线的性质可得DE=DF，然后根据HL可证Rt△BDE≌Rt△CDF，即可证明BE=CF．
试题解析：相等.
理由是：∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF,∠DEB=∠DFC=90°，
在Rt△BDE和Rt△CDF中，
，
∴Rt△BDE≌Rt△CDF(HL)，
∴BE=CF. 如图，已知AB＝AC=12 cm，AE=AF=7 cm，CE=10 cm，△ABF的周长是_________.
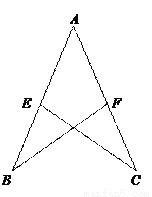
29cm
【解析】∵AB=AC，AE=AF=7（已知），∠A=∠A（公共角）
∴△ABC≌△ACE（SAS）
∴BF=CE=10 cm，
∴△ABF的周长＝AB+BF+FA＝12+7+10＝29(cm)
故答案为：29cm. 在下列说法中，正确的有（ ）个．
①三角对应相等的两个三角形全等；②三边对应相等的两个三角形全等；③两角，一边对应相等的两个三角形全等；④两边，一角对应相等的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
B
【解析】①三角对应相等的两个三角形不一定全等，错误；
②三边对应相等的两个三角形全等，正确；
③两个角和其中一角的对边对应相等的两个三角形全等，正确；
④两条边和其中一边的对角对应相等的两个三角形不一定全等，错误；
故选：B 已知x2＋3x－1=0，求x－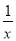
和x2＋
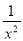的值．
－3,11
【解析】分析：首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析：
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为：-3，,11. 若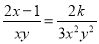
，则k的值为 （ ）
A. 3x2y2(2x-1) B. 
xy(2x-1) C. 
xy2(2x-1) D. xy2(2x-1)
B
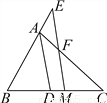
【解析】∵, ∴2k=,∴k= (6x²y-3xy)= xy(2x-1).故选B. 如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F.
(1)求证：AE＝AF；
(2)求证：BE＝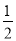
(AB＋AC)．
（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据角平分线的性质及平行线的性质易∠AEF=∠AFE，即可得AE=AF；（2）作CG∥EM，交BA的延长线于G，已知AC=AG，根据三角形中位线定理的推论证明BE=EG，再利用三角形的中位线定理即可证得结论．
试题解析：
（1）∵DA平分∠BAC，
∴∠BAD=∠CAD，
∵AD∥EM，
∴∠BAD=...