题目内容
已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
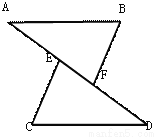
A. SSS B. SAS C. ASA D. HL
 D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.
D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC.
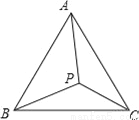
 证明见解析.
【解析】试题分析:运用反证法进行求解.
试题解析:证明:假设PB≠PC不成立,则PB=PC.
在△ABP和△ACP中,∵AB=AC,AP=AP,BP=CP,∴△ABP≌△ACP,∴∠APB=∠APC.
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC.
证明见解析.
【解析】试题分析:运用反证法进行求解.
试题解析:证明:假设PB≠PC不成立,则PB=PC.
在△ABP和△ACP中,∵AB=AC,AP=AP,BP=CP,∴△ABP≌△ACP,∴∠APB=∠APC.
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC. 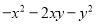 =__________
=__________
 【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: .
【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为: .
故答案为: . 下列多项式中,能用公式法分解因式的是( )
A. m2-mn B. m2+mn C. m2-n2 D. m2+n2
 C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C.
C
【解析】根据平方差公式的特点: ,可知C符合题意.
故选:C. 已知:如图,点C为AB中点,CD=BE,CD∥BE.求证:△ACD≌△CBE.
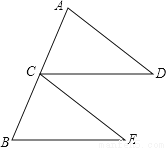
 证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS)
证明见解析.
【解析】试题分析:根据中点定义求出AC=CB,根据两直线平行,同位角相等,求出∠ACD=∠B,然后利用SAS即可证明△ACD≌△CBE.
试题解析:证明:∵CD∥BE,∴∠ACD=∠B..
∵点C为AB中点,∴AC=CB.
又∵CD=BE,∴△ACD≌△CBE(SAS) 如图,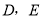 分别为
分别为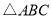 的
的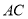 ,
,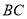 边的中点,将此三角形沿
边的中点,将此三角形沿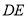 折叠,使点
折叠,使点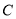 落在
落在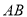 边上的点
边上的点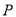 处.若
处.若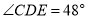 ,则
,则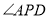 等于( )
等于( )
A.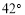 B.
B.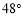 C.
C.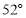 D.
D.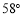
 B
【解析】
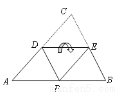
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=.
B
【解析】
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=. 如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )
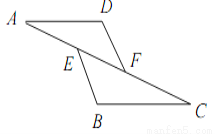
A. ∠A=∠C B. AD=CB C. BC=DF D. DF∥BE
 C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C.
C
【解析】∵AE=CF(已知),
∴AE+EF=EF+CF,
∴AF=EC,
∵∠AFD=∠CEB,
∴△AFD≌△CEB(SAS),
∴∠A=∠C,
AD=CB,BC=DA,
∵∠AFD=∠CEB,
∴DF∥BE.
故选:C. 当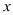 为任意实数时,下列分式中一定有意义的是( )
为任意实数时,下列分式中一定有意义的是( )
A. 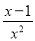 B.
B. 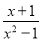 C.
C. 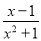 D.
D. 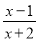
 C
【解析】A.当x=0时,x²=0,分式无意义;
B.当x=±1时,x²-1=0,分式无意义;
C.当x为任意实数时,x²+1≠0,分式有意义;
D.当x=-2时,x+2=0,分式无意义.
故选C.
C
【解析】A.当x=0时,x²=0,分式无意义;
B.当x=±1时,x²-1=0,分式无意义;
C.当x为任意实数时,x²+1≠0,分式有意义;
D.当x=-2时,x+2=0,分式无意义.
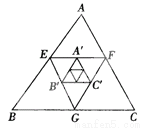
故选C. 如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.
 16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长...
16
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=BC,EG=AC,FG=AB,
∴EF+FG+EG=(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为×64=16,
以此类推,第n个小三角形的周长... 
