题目内容
如图,AC=AD,BC=BD,则有( )
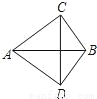
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
 A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.
A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是__________.
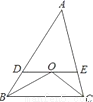
 9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A...
9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A... 若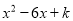 是一个完全平方式,那么k=_______________
是一个完全平方式,那么k=_______________
 9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9.
9
【解析】因为若是一个完全平方式,那么,那么答案是k=9.
故答案为:9. 下列多项式能用完全平方公式分解因式的是( )
A. 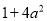 B.
B. 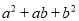 C.
C. 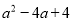 D.
D. 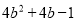
 C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C.
C
【解析】根据完全平方公式: ,可以进行判断出答案是C选项正确.
故选:C. 如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
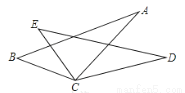
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定. 下列说法正确的是( )
A. 两个周长相等的长方形全等 B. 两个周长相等的三角形全等
C. 两个面积相等的长方形全等 D. 两个周长相等的圆全等
 D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D.
D
【解析】A.长方形周长相等,但面积、长、宽不一定相等,错;
B.三角形周长相等,但不一定对应边完全相等,错;
C.长方形面积相等,但长、宽不一定相等,错;
D.圆的周长相等,就可知道半径相等,两圆可完全重合,正确。
故选:D. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
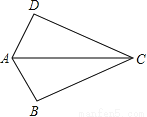
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
 C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC...
C
【解析】试题分析:本题要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能. A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC... 化简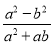 的结果为( )
的结果为( )
A. 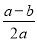 B.
B. 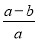 C.
C. 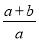 D.
D. 
 B
【解析】=,故选B.
B
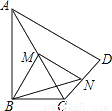
【解析】=,故选B. 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
 (1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=...
(1)证明见解析;(2)
【解析】试题分析:(1)在△CAD中,由中位线定理得到MN∥AD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN90°,得到,再由MN=... 
