��Ŀ����
��ͼ����֪AB��CD��AB=CD,AE=FD,��ͼ�е�ȫ���������У� ��
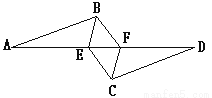
A. 1�� B. 2�� C. 3�� D. 4��
 C
����������AB��CD��
���A=��D��
��AB=CD��AE=FD��
���ABE�ա�DCF(SAS)��
��BE=CF����BEA=��CFD��
���BEF=��CFE��
��EF=FE��
���BEF�ա�CFE(SAS)��
��BF=CE��
��AE=DF��
��AE+EF=DF+EF��
��AF=DE��
���ABF�ա�CDE(SSS)...
C
����������AB��CD��
���A=��D��
��AB=CD��AE=FD��
���ABE�ա�DCF(SAS)��
��BE=CF����BEA=��CFD��
���BEF=��CFE��
��EF=FE��
���BEF�ա�CFE(SAS)��
��BF=CE��
��AE=DF��
��AE+EF=DF+EF��
��AF=DE��
���ABF�ա�CDE(SSS)...
��ϰ��ϵ�д�
�����Ŀ
��ͼ��AD�ǡ�ABC�ı�BC�ϵĸߣ������������е�ijһ�������Ƴ���ABC�ǵ��������ε���__��
�١�BAD=��ACD���ڡ�BAD=��CAD����AB+BD=AC+CD����AB��BD=AC��CD��
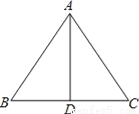
 �ڢۢ�
����������������
Ӧ���ӵ������Ǣڢۢܣ�
֤�����ڵ���BAD=��CADʱ����AD�ǡ�BAC��ƽ���ߣ���AD��BC���ϵĸߣ����ABD�ա�ACD�����BAC�ǵ��������Σ�
���ӳ�DB��E��ʹBE=AB���ӳ�DC��F��ʹCF=AC������AE��AF��
��AB+BD=CD+AC����DE=DF����AD��BC�����AEF�ǵ��������Σ����E=��F��
��AB=BE�����A...
�ڢۢ�
����������������
Ӧ���ӵ������Ǣڢۢܣ�
֤�����ڵ���BAD=��CADʱ����AD�ǡ�BAC��ƽ���ߣ���AD��BC���ϵĸߣ����ABD�ա�ACD�����BAC�ǵ��������Σ�
���ӳ�DB��E��ʹBE=AB���ӳ�DC��F��ʹCF=AC������AE��AF��
��AB+BD=CD+AC����DE=DF����AD��BC�����AEF�ǵ��������Σ����E=��F��
��AB=BE�����A... �ֽ���ʽ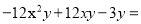 ___________
___________
 ��������������ʽ�ֽ�ķ��������ṫ��ʽ-3y���ٸ�����ȫƽ����ʽ�ֽ���ʽΪ�� .
�ʴ�Ϊ�� .
��������������ʽ�ֽ�ķ��������ṫ��ʽ-3y���ٸ�����ȫƽ����ʽ�ֽ���ʽΪ�� .
�ʴ�Ϊ�� . ���ж���ʽ�����ù�ʽ���ֽ���ʽ���У� ��
��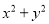 ��
��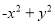 ��
��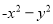 ��
��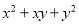
��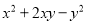 ��
��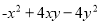
A. 2�� B. 3�� C. 4�� D. 5��
 A
��������������ȫƽ����ʽ,ƽ���ʽ,
���������ж��ڿ�������ƽ���ʽ������ʽ�ֽ�,����������ȫƽ����ʽ������ʽ�ֽ�,��˱�����ȷѡ����A.
A
��������������ȫƽ����ʽ,ƽ���ʽ,
���������ж��ڿ�������ƽ���ʽ������ʽ�ֽ�,����������ȫƽ����ʽ������ʽ�ֽ�,��˱�����ȷѡ����A. ����ͼ��ʾ��2��2�����У�����AB��AC�����1+��2=_____�ȣ�
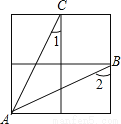
 90��
���������ڡ�ACM�͡�BAN�У�AN=CM����AMC=��BNA��CM=AN
���ACM�ա�BAN��
���2=��CAM�����ɵá�1+��2=90�㣮�ʴ�Ϊ��90��.
90��
���������ڡ�ACM�͡�BAN�У�AN=CM����AMC=��BNA��CM=AN
���ACM�ա�BAN��
���2=��CAM�����ɵá�1+��2=90�㣮�ʴ�Ϊ��90��. ʹ����ֱ��������ȫ�ȵ������ǣ� ��
A. һ��Ƕ�Ӧ��� B. ����Ƕ�Ӧ��� C. һ���߶�Ӧ��� D. �����߶�Ӧ���
 D
���������������������ȫ�������ε��ж���ȷ��������ʱ��Ҫ�����֪������������ȫ�ȵ��ж����������֤��
��������
A��һ����Ƕ�Ӧ��ȣ�������֪��ֱ����ȣ��ɵó���һ�������ȣ�������֤����������ȫ�ȣ���Aѡ�����
B�����������ȣ���ôҲ����������Ӧ����ȣ�������֤����������ȫ�ȣ���Bѡ�����
C��һ���߶�Ӧ��ȣ��ټ�һ��ֱ����ȣ����ܵó���������ȫ�ȣ���Cѡ���...
D
���������������������ȫ�������ε��ж���ȷ��������ʱ��Ҫ�����֪������������ȫ�ȵ��ж����������֤��
��������
A��һ����Ƕ�Ӧ��ȣ�������֪��ֱ����ȣ��ɵó���һ�������ȣ�������֤����������ȫ�ȣ���Aѡ�����
B�����������ȣ���ôҲ����������Ӧ����ȣ�������֤����������ȫ�ȣ���Bѡ�����
C��һ���߶�Ӧ��ȣ��ټ�һ��ֱ����ȣ����ܵó���������ȫ�ȣ���Cѡ���... ��ͼ��AB=AC��������������������SAS�жϡ�ABE�ա�ACD���ǣ�������
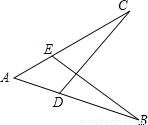
A. ��B=��C B. ��AEB=��ADC C. AE=AD D. BE=DC
 C
����������AB=AC ����֪������A=��A�������ǣ���
��ֻ��ҪAE=AD��
���ABE�ա�ACD��
��ѡ��C.
C
����������AB=AC ����֪������A=��A�������ǣ���
��ֻ��ҪAE=AD��
���ABE�ա�ACD��
��ѡ��C. ��֪����ʽ�� 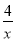 ��
��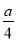 ��
��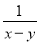 ��
��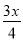 ��
��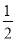 x2��
x2�� ��4�����з�ʽ�� �� ��
��4�����з�ʽ�� �� ��
A. 2�� B. 3�� C. 4�� D. 5��
 B
��������������x2�ķ�ĸ�о���������ĸ,�����������ʽ,�����Ƿ�ʽ.
��������4�ķ�ĸ�к�����ĸ,����Ƿ�ʽ.
����Bѡ������ȷ��.
B
��������������x2�ķ�ĸ�о���������ĸ,�����������ʽ,�����Ƿ�ʽ.
��������4�ķ�ĸ�к�����ĸ,����Ƿ�ʽ.
����Bѡ������ȷ��. (1)�����ε���λ�ߵĶ��壺��������������____________���������ε���λ�ߣ�
(2)�����ε���λ�߶����������ε���λ��________�����ߣ����ҵ���___________��
 (1)�е���߶�; (2)ƽ���������ε� �����ߵ�һ��
��������(1)�����ε���λ�ߵĶ��壺���������������е���߶ν��������ε���λ�ߣ�
�ʴ�Ϊ���е���߶Σ�
(2)�����ε���λ�߶����������ε���λ��ƽ���������εĵ����ߣ����ҵ��ڵ����ߵ�һ�룬
�ʴ�Ϊ��ƽ���������εģ������ߵ�һ��.
(1)�е���߶�; (2)ƽ���������ε� �����ߵ�һ��
��������(1)�����ε���λ�ߵĶ��壺���������������е���߶ν��������ε���λ�ߣ�
�ʴ�Ϊ���е���߶Σ�
(2)�����ε���λ�߶����������ε���λ��ƽ���������εĵ����ߣ����ҵ��ڵ����ߵ�һ�룬
�ʴ�Ϊ��ƽ���������εģ������ߵ�һ��. 
