题目内容
如图，△ABC≌△CDA,且AD＝CB，下列结论错误的是（ ）
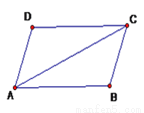
A. ∠B＝∠D B. ∠CAB＝∠ACD C. BC＝CD D. AC＝CA
C
【解析】∵△ABC≌△CDA，
∴∠CAB＝∠ACD，CA=AC，∠D=∠B，故A. B.D正确，不符合题意，
BC不一定等于CD，C错误，符合题意，
故选：C.
练习册系列答案
备战中考寒假系列答案
相关题目
如图,一艘海轮位于灯塔P南偏东70°方向的M处,它以每时40海里的速度向正北方向航行,2时后到达位于灯塔P北偏东40°方向的N处,则N处与灯塔P的距离为( )
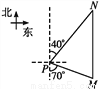
A. 40海里 B. 60海里
C. 70海里 D. 80海里
D
【解析】试题解析：MN=2×40=80（海里），
∵∠M=70°，∠N=40°，
∴∠NPM=180°-∠M-∠N=180°-70°-40°=70°，
∴∠NPM=∠M，
∴NP=MN=80（海里）．
故选D． 因式分解: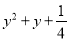 
=______
【解析】根据完全平方公式进行因式分解为： .
故答案为：
. 如图，已知AB=AC，E，D分别是AB，AC的中点，且AF⊥BD交BD的延长线于F，AG⊥CE交CE的延长线于G，试判断AF和AG的关系是否相等，并说明理由．
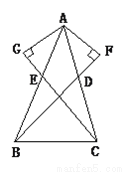
AF=AG
【解析】试题分析：先由SAS证得△ABD≌△ACE，由全等三角形对应边相等得∠ABD=∠ACE，由AAS证得△ABF≌△ACG，即可证得AF=AG.
试题解析：
∵AB=AC，E，D分别是AB，AC的中点，
∴ AD=AE.
∴在△ABD和△ACE中，
∴△ABD≌△ACE (SAS)．
∴∠ABD=∠ACE，
在△ABF和△ACG中，
... 如图，MN与PQ相交于点O，MO=OP，QO=ON，∠M=65°，∠Q=30°，则∠P=____，∠N=___.
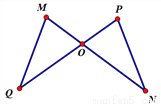
65° 30°
【解析】∵MO=OP，QO=ON（已知），
∠MO Q=∠PO N（对顶角相等）
∴△MOQ≌△PON（SAS）
∴∠P=∠M=65°，
∠N=∠Q=30°
故答案为：65°；30° 在下列条件中，不能说明△ABC≌△A’B’C’的是( )
A. ∠A＝∠A’，∠C＝∠C’，AC＝A’C’ B. ∠A＝∠A’，AB＝A’B’，BC＝B’C’
C. ∠B＝∠B’，∠C＝∠C’，AB＝A’B’ D. AB＝A’B’， BC＝B’ C’AC＝A’C’
B
【解析】A、∠A=∠A′，∠C=∠C′，AC=A′C′，可用ASA判定△ABC≌△A′B′C，故选项正确；
B、∠A=∠A′，AB=A′B′，BC=B′C′，SSA不能判定两个三角形全等，故选项错误；
C、∠B=∠B′，∠C=∠C′，AB=A′B′，可用AAS判定△ABC≌△A′B′C，故选项正确；
D、AB=A′B′，BC=B′C，AC=A′C′，可用ASA判定△AB... 若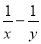
=3 ，求
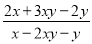的值．
【解析】分析：由已知可知x-y=-3xy，然后代入所求的式子，进行约分就可求出结果．
本题解析：
∵ =3，∴y-x=3xy, ∴x-y=-3xy,
∴ =. 若代数式
的值为零，则x的值为（ ）
A. 2或-1 B. -1 C. ±1 D. 2
D
【解析】根据题意得:(x-2)(x+1)=0,且 ,
计算得出:x=2,
所以D选项是正确的. 如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
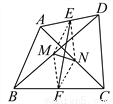
证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
...