题目内容
如图,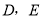 分别为
分别为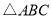 的
的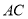 ,
,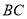 边的中点,将此三角形沿
边的中点,将此三角形沿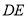 折叠,使点
折叠,使点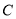 落在
落在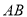 边上的点
边上的点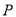 处.若
处.若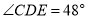 ,则
,则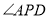 等于( )
等于( )
A.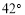 B.
B.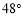 C.
C.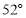 D.
D.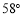
 B
【解析】
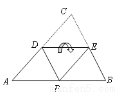
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=.
B
【解析】
试题分析:因为分别为的,边的中点,所以DE是的中位线
所以DE∥BC,所以∠APD=∠EDP,由折叠可知:∠EDP =,所以=.
练习册系列答案
相关题目
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
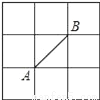
A. 6 B. 7 C. 8 D. 9
 C
【解析】试题分析:如图:分情况讨论
①AB为等腰△ABC底边时,符合条件的C点有2个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选A.
C
【解析】试题分析:如图:分情况讨论
①AB为等腰△ABC底边时,符合条件的C点有2个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选A. ______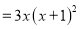
 【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: .
【解析】根据因式分解与整式乘法的互逆性,可知直接进行乘法计算为: =.
故答案为: . 已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
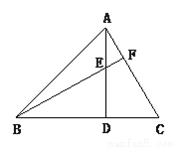
 BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE...
BE⊥AC
【解析】试题分析:在直角△BED与△ACD中,根据HL判定△BED≌ACD,根据全等三角形的对应角相等,得出∠DBE=∠DAC,再根据AD是高线,结合∠BED=∠AEF,进而推出∠DAC+∠AEF=90°,据此可得结论.
试题解析:BF⊥AC.理由如下:
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵在直角△BED与△ACD中,BE=AC,DE... 已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
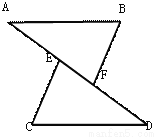
A. SSS B. SAS C. ASA D. HL
 D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D.
D
【解析】∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD,
∴Rt△ABF≌Rt△DCE(HL)
故选:D. 如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
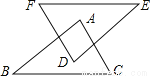
A. 40° B. 50° C. 60° D. 70°
 D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D .
D
【解析】∵∠E=40°,∠F=70°,
∴∠D =70°,
∵FE=BC,DE=AB,∠B=∠E=40°,
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°.
故选:D . 先化简,后求值: 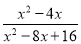 ,其中x=5.
,其中x=5.
 5
【解析】原式=,
把x=5代入得,原式=5.
5
【解析】原式=,
把x=5代入得,原式=5. 下列分式中,当x=1时,有意义的是( )
①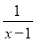 ;②
;②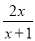 ;③
;③ ;④
;④ .
.
A. ①③ B. ①②③ C. ②③ D. ②④
 D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
综上所述,当x=1时,分式、有意义.故选D.
D
【解析】对于①,要使有意义,则x-1≠0,则x≠1;
对于②,要使有意义,则x+1≠0,则x≠-1;
对于③,要使有意义,则(x-1)(x-2)≠0,即x≠1且x≠2;
对于④,要使.)有意义,则(x+1)(x+2)≠0,则x≠-1且x≠-2.
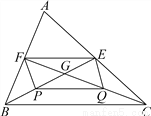
综上所述,当x=1时,分式、有意义.故选D. 如图,△ABC的中线BE,CF相交于点G,P、Q分别是BG、CG的中点.
(1)求证:四边形EFPQ是平行四边形;
(2)请直接写出BG与GE的数量关系.(不要求证明).
 (1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是...
(1)证明见解析;(2)BG=2GE.
【解析】试题分析:(1)根据BE,CF是△ABC的中线可得EF是△ABC的中位线,P,Q分别是BG,CG的中点可得PQ是△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=BC,PQ∥BC且PQ=BC,进而可得EF∥PQ且EF=PQ,根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)根据平行四边形的性质可得GE=GP,再根据P是... 
