题目内容
使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
 D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...
D
【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【解析】
A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;
B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;
C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...
练习册系列答案
相关题目
如图,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F的度数是( )
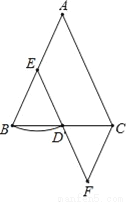
A. 40 B. 70 C. 50 D. 45
 A
【解析】【解析】
∵以点E为圆心,EB为半径画弧,交BC于点D,∴EB=ED,∴∠EDB=∠B=70°,∴∠BED=180°﹣∠B=∠BDE=40°.
∵AB=AC,∴∠ACB=∠B,∴∠EDB=∠ACB,∴EF∥AC.
∵E是AB的中点,即BE=AE,∴BD=CD.
在△EBD和△FCD中,∵DE=DF,∠EDB=∠CDF,BD=CD,∴△EBD≌△FCD(SAS)...
A
【解析】【解析】
∵以点E为圆心,EB为半径画弧,交BC于点D,∴EB=ED,∴∠EDB=∠B=70°,∴∠BED=180°﹣∠B=∠BDE=40°.
∵AB=AC,∴∠ACB=∠B,∴∠EDB=∠ACB,∴EF∥AC.
∵E是AB的中点,即BE=AE,∴BD=CD.
在△EBD和△FCD中,∵DE=DF,∠EDB=∠CDF,BD=CD,∴△EBD≌△FCD(SAS)... 分解因式 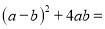 _____________
_____________
 【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: .
【解析】根据完全平方公式进行相乘,合并同类项之后再利用完全平方公式因式分解为: .
故答案为: . 如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
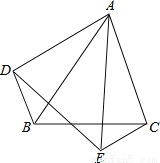
 证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等.
证明见解析.
【解析】试题分析:观察图形,由∠BAC=∠DAE易证∠BAD=∠CAE,然后根据SAS证明三角形全等. 如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
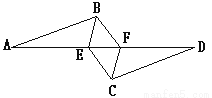
A. 1对 B. 2对 C. 3对 D. 4对
 C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)...
C
【解析】∵AB∥CD,
∴∠A=∠D,
∵AB=CD,AE=FD,
∴△ABE≌△DCF(SAS),
∴BE=CF,∠BEA=∠CFD,
∴∠BEF=∠CFE,
∵EF=FE,
∴△BEF≌△CFE(SAS),
∴BF=CE,
∵AE=DF,
∴AE+EF=DF+EF,
即AF=DE,
∴△ABF≌△CDE(SSS)... 如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )
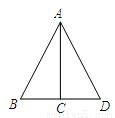
A. AB=AD B. AB=BD C. ∠B=∠D D. AC平分∠BAD
 B
【解析】∵AC⊥BD,点C是BD的中点,
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD,
故选:B .
B
【解析】∵AC⊥BD,点C是BD的中点,
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD,
故选:B . 不改变分式的值,使下列分式的分子和分母的最高次项的系数为正数.
(1)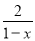 ; (2)
; (2)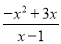 ; (3)
; (3)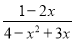 .
.
 (1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) =
(1)- . (2)- . (3)
【解析】根据分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变可得:(1) =- ;
(2) =
(3) = 在代数式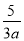 ,
, 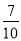 ,
, 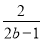 ,
, 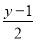 ,x+
,x+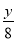 中,是分式的有( )
中,是分式的有( )
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】在代数式, ,, ,x+的分母中均不含有字母,因此它们是整式,而不是分式.
而,分母中含有字母,因此是分式.
故选B.
B
【解析】在代数式, ,, ,x+的分母中均不含有字母,因此它们是整式,而不是分式.
而,分母中含有字母,因此是分式.
故选B. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是__.
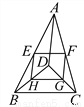
 11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11.
11
【解析】试题解析:∵BD⊥DC,BD=4,CD=3,由勾股定理得,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴HG=BC=EF,EH=FG=AD,
∵AD="6,"
∴EF="HG=2.5,EH=GF=3,"
∴四边形EFGH的周长是EF+FG+HG+EH=2×(2.5+3)=11. 
