在直角三角形中，其中一个锐角是另一个锐角的2倍，则此三角形中最小的角是（ ）
A. 15° B. 30° C. 60° D. 90°
B
【解析】【解析】
设较小的锐角是x°，则另一个锐角是2x°．
由题意得：x+2x=90，解得x=30．
即此三角形中最小的角是30°．
故选B． 直角三角形两锐角的平分线所夹的钝角的度数为（ ）
A. 100度 B. 120度 C. 135度 D. 140度
C
【解析】【解析】
如图，∵∠C=90°，∴∠BAC+∠ABC=180°﹣90°=90°．
∵AD、BE分别是∠BAC和∠ABC的平分线，∴∠OAB+∠OBA=×90°=45°，
∴∠AOB=180°﹣（∠OAB+∠OBA）=180°﹣45°=135°．故选C． 如图所示，H是△ABC的高AD，BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中正确的有（ ）
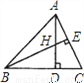
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】【解析】
①∵BE⊥AC，AD⊥BC，∴∠AEH=∠ADB=90°．
∵∠HBD+∠BHD=90°，∠EAH+∠AHE=90°，∠BHD=∠AHE，∴∠HBD=∠EAH．
∵DH=DC，∴△BDH≌△ADC（AAS），∴BD=AD，BH=AC；
②∵BC=AC，∴∠BAC=∠ABC．
由①知，在Rt△ABD中，∵BD=AD，∴∠ABC=45°，∴∠BAC... 如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（ ）
A. SSS B. AAS C. SAS D. HL
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等，这为“边角边”定理，简写成“SAS”．故选C． 如图，在△ABC中，∠C=60°，∠B=50°，D是BC上一点，DE⊥AB于点E，DF⊥AC于点F，则∠EDF的度数为（ ）
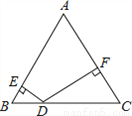
A. 90° B. 100° C. 110° D. 120°
C
【解析】【解析】
在△ABC中，∵∠C=60°，∠B=50°，∴∠A=70°．
∵DE⊥AB于点E，DF⊥AC于点F，∴∠AED=∠AFD=90°，∴∠EDF=360°﹣∠A﹣∠AED﹣∠AFD=110°．故选C． 已知，如图，△ABC中，∠BAC=90°，AD⊥BC于D，则图中相等的锐角的对数有（ ）
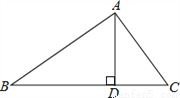
A. 4对 B. 3对 C. 2对 D. 1对
C
【解析】【解析】
相等的锐角有：∠B=∠CAD，∠C=∠BAD共2对．故选C． 下列说法错误的是（ ）
A. 直角三角板的两个锐角互余
B. 经过直线外一点只能画一条直线与已知直线平行
C. 如果两个角互补，那么，这两个角一定都是直角
D. 平行于同一条直线的两条直线平行
C
【解析】解：A．直角三角形中的两个锐角互余，所以直角三角板的两个锐角互余，故本选项说法正确；
B．根据平行公理可知：过直线外一点作已知直线的平行线，能作且只能作一条，故本选项说法正确；
C．如果两个角互补，那么，这两个角和一定是180°，但是它们不一定都是直角，故本选项说法错误；
D．根据平行线的传递性知平行于同一条直线的两条直线平行．故本选项说法正确．
故选C．... 如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：_____________，使△AEH≌△CEB．
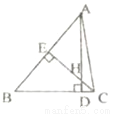
AH＝BC或EA＝EC或EH＝EB等；
【解析】∵AD⊥BC，CE⊥AB，垂足分别为D、E，
∴∠BEC=∠AEC=90°，
在Rt△AEH中，∠EAH=90°﹣∠AHE，
又∵∠EAH=∠BAD，
∴∠BAD=90°﹣∠AHE，
在Rt△AEH和Rt△CDH中，∠CHD=∠AHE，
∴∠EAH=∠DCH，
∴∠EAH=90°﹣∠CHD=∠BCE，
... 如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是______．
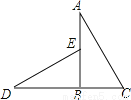
AC=DE
【解析】用“HL”判定△ABC≌△DBE，已知BC=BE，再添加斜边DE=AC即可. 如图，在Rt△ABC中，AC⊥BC，CD⊥AB，∠1=∠2，有下列结论：（1）AC∥DE；（2）∠A=∠3；（3）∠B=∠1；（4）∠B与∠2互余；（5）∠A=∠2．其中正确的有 （填写所有正确的序号）．
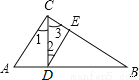
(1)、(2)、(3)
【解析】
试题分析：根据∠1=∠2，即内错角相等，两直线平行可得AC∥DE，则①正确；根据∠1+∠3=∠1+∠A=90°可得∠3=∠A，则②正确；根据∠1+∠3=∠3+∠B=90°可得∠B=∠1，则③正确；根据平行可得DE⊥BC，则∠3+∠2=∠B+∠3=90°，则∠2=∠B，则④错误；根据∠1=∠2，∠1≠∠A可得∠2≠∠A，则⑤错误.