题目内容
如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（ ）
A. SSS B. AAS C. SAS D. HL
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等，这为“边角边”定理，简写成“SAS”．故选C．
练习册系列答案
53随堂测系列答案
相关题目
若关于x的方程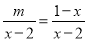
有增根，则m的值为( )
A. 0 B. 1 C. －1 D. 2
C
【解析】试题解析：方程两边同乘以x?2，得
①
∵原方程有增根，
∴x?2=0，
即x=2.
把x=2代入①，得
m=?1.
故选C. 多项式15m3n2+5m2n﹣20m2n3的公因式是（ ）
A. 5mn B. 5m2n2 C. 5m2n D. 5mn2
C
【解析】多项式15n²+5m²n?20m² 中，
各项系数的最大公约数是5，
各项都含有的相同字母是m、n，字母m的指数最低是2，字母n的指数最低是1，
所以它的公因式是5m²n.
故选C. 如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B；求证：CD⊥AB；
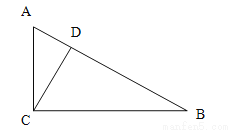
证明过程见解析
【解析】试题分析：根据∠ACB=90°得出∠A+∠B=90°，结合已知条件得出∠A+∠ACD=90°，从而得出答案.
试题解析：∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB 如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是______．
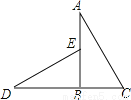
AC=DE
【解析】用“HL”判定△ABC≌△DBE，已知BC=BE，再添加斜边DE=AC即可. 如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
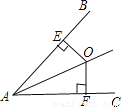
A.HL B.AAS C.SSS D.ASA
A
【解析】
试题分析：利用点O到AB，AC的距离OE=OF，可知△AEO和△AFO是直角三角形，然后可直接利用HL求证△AEO≌△AFO，即可得出答案．
【解析】
∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO．
故选A． 如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，CE=BC，过点E作AC的垂线，交CD的延长线于点F．求证：AB=FC．
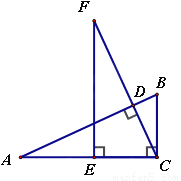
见解析证明．
【解析】
试题分析：利用同角的余角相等得到一对角相等，再由一对直角相等，夹边EC=BC，利用AAS得到△FEC与△ACB全等，利用全等三角形对应边相等即可得证．
试题解析：∵EF⊥AC，∴∠FEC=90°=∠ACB，∴∠F +∠FCE= 90°，∵CD⊥AB，∴∠ADC=90°，∴∠A +∠FCE =90°， ∴∠F=∠A，在△FEC和△ACB中，∵，∴△FEC≌△... 要画出某一图形平移后的图形，必须知道_____和_____
方向 距离
【解析】试题解析：平移前后两个图形全等，但是要画出来的话必须知道平移的方向和距离.
故答案为：(1). 方向 (2). 距离. 下列数值中不是不等式5x≥2x+9的解的是（ ）
A. 5 B. 4 C. 3 D. 2
D
【解析】试题解析：移项得，5x﹣2x≥9,
合并同类项得，3x≥9,
系数化为1得，x≥3,
所以，不是不等式的解集的是x=2．
故选D．