题目内容
如图，已知AB⊥CD，垂足为B，BC=BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加的一个条件是______．
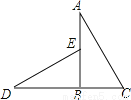
AC=DE
【解析】用“HL”判定△ABC≌△DBE，已知BC=BE，再添加斜边DE=AC即可.
练习册系列答案
相关题目
解方程：
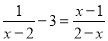
x＝3
【解析】试题分析：按照解分式方程的步骤解方程即可.
试题解析：去分母，得
去括号，得
移项，得
合并同类项，得
系数化为1，得
检验：当时，
是原方程的解. 4x(m－n)＋8y(n－m)2中各项的公因式是________.
4(m－n)
【解析】根据题意，先变形为4x(m－n)＋8y(m－n)2，把m-n看做一个整体，即可找到公因式4（m-n）.
故答案为：4（m-n）. 如图所示，△DEF是由△ABC经过平移得到的，若∠B=50°,∠C=75°,则∠D=_____，∠E＝________.
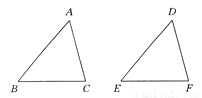
55° 50°
【解析】试题分析：在△ABC中，∠A＝180°－∠B－∠C＝55°，
由平移的性质可知：∠D＝∠A＝55°，∠E＝∠B＝50°，
故答案为：55°，50°． 已知：AB⊥BC，AD⊥DC，∠1=∠2，问：△ABC≌△ADC吗？说明理由．
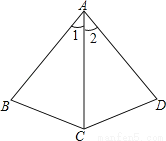
见解析
【解析】试题分析：根据全等三角形的判定定理AAS进行证明．
试题解析：【解析】
△ABC≌△ADC．理由如下：
∵AB⊥BC，AD⊥DC，∴∠B=∠D=90°．
在△ABC与△ADC中，∵，∴△ABC≌△ADC（AAS）． 如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（ ）
A. SSS B. AAS C. SAS D. HL
C
【解析】【解析】
两边及夹角对应相等的两个三角形全等，这为“边角边”定理，简写成“SAS”．故选C． 如图，若要用“HL”证明Rt△ABC≌Rt△ABD，则还需补充条件（ ）
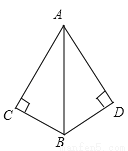
A. ∠BAC=∠BAD B. AC=AD或BC=BD
C. AC=AD且BC=BD D. 以上都不正确
B
【解析】试题解析：从图中可知AB为Rt△ABC和Rt△ABD的斜边，也是公共边．
很据“HL”定理，证明Rt△ABC≌Rt△ABD，
还需补充一对直角边相等，
即AC=AD或BC=BD，
故选B． 三角形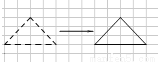
右边的是由左边的怎样平移得到的？
向右平移7个单位.
【解析】试题分析:观察图形中对应点的变化，即可得出图形的变化规律.
试题解析：
找出对应点来后会发现右边的图形是由左边的向右平移7个单位长度得到的. 如果式子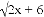
有意义，那么x的取值范围在数轴上表示出来，正确的是（ ）
A. 
B. 
C. 
D. 
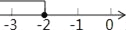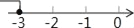
C
【解析】试题分析：先根据二次根式的意义，其有意义的条件是被开方数大于等于0，因此可得2x+6≥0，可解不等式得x≥-3，因此可在数轴上表示为C.
故选C