题目内容
直角三角形两锐角的平分线所夹的钝角的度数为（ ）
A. 100度 B. 120度 C. 135度 D. 140度
C
【解析】【解析】
如图，∵∠C=90°，∴∠BAC+∠ABC=180°﹣90°=90°．
∵AD、BE分别是∠BAC和∠ABC的平分线，∴∠OAB+∠OBA=×90°=45°，
∴∠AOB=180°﹣（∠OAB+∠OBA）=180°﹣45°=135°．故选C．
分式方程
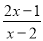=1的解为（ ）
A. x=﹣1 B. x=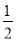
C. x=1 D. x=2
A
【解析】【解析】
去分母得：2x﹣1=x﹣2，
解得：x=﹣1，
经检验x=﹣1是分式方程的解，
则分式方程的解为x=﹣1．
故选：A． 在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形．依照图中标注的数据，请你计算空白部分的面积．
ab – ac – bc ＋ c2
【解析】试题分析：把②向左平移c，④向上平移c，③先向上平移c，再向左平移c，使①②③④拼成一个长为(a－c)，宽为(b－c)的矩形，然后根据矩形的面积公式进行计算即可．
试题解析：
如图，将四块空白部分向①拼拢（即平移），这样就形成了一个长为(a－c)，宽为(b－c)的矩形．
∴S空白＝(a－c)×(b－c)＝ab – ac – bc ... 已知：AB⊥BC，AD⊥DC，∠1=∠2，问：△ABC≌△ADC吗？说明理由．
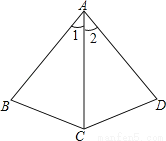
见解析
【解析】试题分析：根据全等三角形的判定定理AAS进行证明．
试题解析：【解析】
△ABC≌△ADC．理由如下：
∵AB⊥BC，AD⊥DC，∴∠B=∠D=90°．
在△ABC与△ADC中，∵，∴△ABC≌△ADC（AAS）． 下列说法错误的是（ ）
A. 直角三角板的两个锐角互余
B. 经过直线外一点只能画一条直线与已知直线平行
C. 如果两个角互补，那么，这两个角一定都是直角
D. 平行于同一条直线的两条直线平行
C
【解析】解：A．直角三角形中的两个锐角互余，所以直角三角板的两个锐角互余，故本选项说法正确；
B．根据平行公理可知：过直线外一点作已知直线的平行线，能作且只能作一条，故本选项说法正确；
C．如果两个角互补，那么，这两个角和一定是180°，但是它们不一定都是直角，故本选项说法错误；
D．根据平行线的传递性知平行于同一条直线的两条直线平行．故本选项说法正确．
故选C．... 如图，若要用“HL”证明Rt△ABC≌Rt△ABD，则还需补充条件（ ）
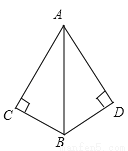
A. ∠BAC=∠BAD B. AC=AD或BC=BD
C. AC=AD且BC=BD D. 以上都不正确
B
【解析】试题解析：从图中可知AB为Rt△ABC和Rt△ABD的斜边，也是公共边．
很据“HL”定理，证明Rt△ABC≌Rt△ABD，
还需补充一对直角边相等，
即AC=AD或BC=BD，
故选B． 四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
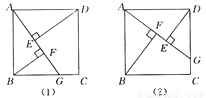
EF＝AF－BF △ABF≌△DAE EF＝BF－AF
【解析】试题分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．
(1) 证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，
∴∠BAF+∠DAE＝90°．
... △
是△
平移后得到的三角形，则△≌△，理由是___________________________
平移前后的两个图形全等
【解析】试题解析：平移前后的两个三角形大小和形状没有发生改变，所以是全等图形.
故答案为：平移前后的两个图形全等. 已知∠AOB及其内部一点P，试讨论以下问题的解答：
（1）如图①，若点P在∠AOB的平分线上，我们可以过P点作直线垂直于角平分线，分别交OA、OB于点C、D，则可以得到△OCD是以CD为底边的等腰三角形；若点P不在∠AOB的平分线上（如图②），你能过P点作直线，分别交OA、OB于点C、D，得到△OCD是等腰三角形，且CD是底边吗？请你在图②中画出图形，并简要说明画法．
（2）若点P不在∠AOB的平分线上（如图③），我们可以过P点作PQ∥OA，并作∠QPR=∠AOB，直线PR分别交OA、OB于点C、D，则可以得到△OCD是以OC为底的等腰三角形．请你说明这样作的理由．
（3）若点P不在∠AOB的平分线上，请你利用在（2）中学到的方法，在图④中过P点作直线分别交OA、OB于点C、D，使得△OCD是等腰三角形，且OD是底边．保留画图的痕迹，不用写出画法．
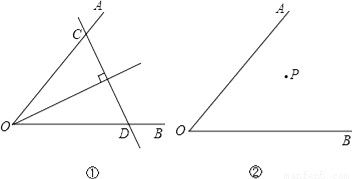
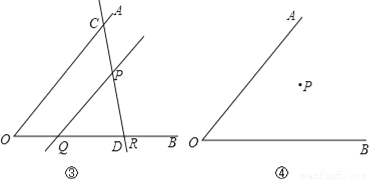
（1）能，画法见解析；（2）理由见解析；（3）见解析.
【解析】试题分析：（1）作∠AOB的平分线，过P点作角平分线的垂线，分别交角的两边OA、OB于点C、D，则△OCD是以CD为底边的等腰三角形；
（2）根据PQ∥OA，得出∠QPR=∠OCD，进而得出OD=CD，即可得出答案；
（3）作QP∥DO，再作∠ODR=∠O，即可得出答案．
试题解析：【解析】
（1）能．
...