��Ŀ����
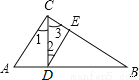
��ͼ����Rt��ABC�У�AC��BC��CD��AB����1=��2�������н��ۣ���1��AC��DE����2����A=��3����3����B=��1����4����B���2���ࣻ��5����A=��2��������ȷ���� ����д������ȷ����ţ���
 (1)��(2)��(3)
��������
������������ݡ�1=��2�����ڴ�����ȣ���ֱ��ƽ�пɵ�AC��DE�������ȷ�����ݡ�1+��3=��1+��A=90��ɵá�3=��A�������ȷ�����ݡ�1+��3=��3+��B=90��ɵá�B=��1�������ȷ������ƽ�пɵ�DE��BC�����3+��2=��B+��3=90�㣬���2=��B����ܴ����ݡ�1=��2����1�١�A�ɵá�2�١�A����ݴ���.
(1)��(2)��(3)
��������
������������ݡ�1=��2�����ڴ�����ȣ���ֱ��ƽ�пɵ�AC��DE�������ȷ�����ݡ�1+��3=��1+��A=90��ɵá�3=��A�������ȷ�����ݡ�1+��3=��3+��B=90��ɵá�B=��1�������ȷ������ƽ�пɵ�DE��BC�����3+��2=��B+��3=90�㣬���2=��B����ܴ����ݡ�1=��2����1�١�A�ɵá�2�١�A����ݴ���.
 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д����ʽ���̣�
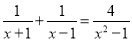
 x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�.
x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�. ��ʽ�֡�������
x2��3x =______________.
 x(x-3)
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3����
x(x-3)
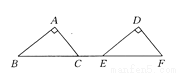
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3���� ��ͼ��ʾ����ABC����ƽ�Ƶõ���DEF����֪CE��2 cm��AC��3 cm��AB��4 cm����A��90�㣬��CF��_________cm��ƽ�Ƶľ�����_________��
 7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
�ʴ�Ϊ��7��7cm��
7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
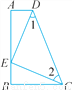
�ʴ�Ϊ��7��7cm�� ��ͼ����A����B��90�㣬E��AB��һ�㣬��AE��BC����1����2.��֤����ADE�ա�BEC.
 ֤��������
������������������ɡ�1=��2���ɵ�DE=CD������֤��ֱ��������ȫ�ȵġ�HL��������֤������.
����������ߡ�1����2��
��DE��EC.
�֡ߡ�A����B��90�㣬AE��BC��
��Rt��ADE��Rt��BEC(HL).
֤��������
������������������ɡ�1=��2���ɵ�DE=CD������֤��ֱ��������ȫ�ȵġ�HL��������֤������.
����������ߡ�1����2��
��DE��EC.
�֡ߡ�A����B��90�㣬AE��BC��
��Rt��ADE��Rt��BEC(HL). ��ͼ���ڡ�ABC�У���C=60�㣬��B=50�㣬D��BC��һ�㣬DE��AB�ڵ�E��DF��AC�ڵ�F�����EDF�Ķ���Ϊ��������
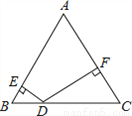
A. 90�� B. 100�� C. 110�� D. 120��
 C
����������������
�ڡ�ABC�У��ߡ�C=60�㣬��B=50�㣬���A=70�㣮
��DE��AB�ڵ�E��DF��AC�ڵ�F�����AED=��AFD=90�㣬���EDF=360�㩁��A����AED����AFD=110�㣮��ѡC��
C
����������������
�ڡ�ABC�У��ߡ�C=60�㣬��B=50�㣬���A=70�㣮
��DE��AB�ڵ�E��DF��AC�ڵ�F�����AED=��AFD=90�㣬���EDF=360�㩁��A����AED����AFD=110�㣮��ѡC�� ���п�ʹ����ֱ��������ȫ�ȵ������ǣ�������
A. һ���߶�Ӧ��� B. ����ֱ�DZ߶�Ӧ���
C. һ����Ƕ�Ӧ��� D. ������Ƕ�Ӧ���
 B
����������������
��ֱ������������һ����������ֱ����ȣ�Ҫ�ж���ֱ��������ȫ�ȣ����뻹Ҫ�����������ʿ��ų�A��C��
��D������AAA�������ж�ȫ�ȣ�
B������SAS�������ж�����ֱ��������ȫ�ȣ�
��ѡB��
B
����������������
��ֱ������������һ����������ֱ����ȣ�Ҫ�ж���ֱ��������ȫ�ȣ����뻹Ҫ�����������ʿ��ų�A��C��
��D������AAA�������ж�ȫ�ȣ�
B������SAS�������ж�����ֱ��������ȫ�ȣ�
��ѡB�� ����ƽ��ֻ�ı�ͼ�ε��Ƿ��棬û�иı�ͼ�ε��ļ����棿
 ����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε���״����С.
���������������������ƽ�Ƶ������ش�.
���������
����ƽ�Ƶ��������Եó�����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε� ��״����С.
����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε���״����С.
���������������������ƽ�Ƶ������ش�.
���������
����ƽ�Ƶ��������Եó�����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε� ��״����С. ��֪x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��x=1�����������ʽ�Ľ⣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A. a��1 B. a��2 C. 1��a��2 D. 1��a��2
 C
������������x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��֪��2-5����2a-3a+2����0����ã�a��2���ٸ���x=1�����������ʽ�Ľ⣬�ɵã�1-5����a-3a+2����0����ã�a��1��
�ɴ˿ɵ�a��ȡֵ��ΧΪ��1��a��2��
��ѡ��C.
C
������������x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��֪��2-5����2a-3a+2����0����ã�a��2���ٸ���x=1�����������ʽ�Ľ⣬�ɵã�1-5����a-3a+2����0����ã�a��1��
�ɴ˿ɵ�a��ȡֵ��ΧΪ��1��a��2��
��ѡ��C. 
