为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B两点之间距离的有( )
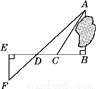
A. 1组 B. 2组 C. 3组 D. 4组
 C
【解析】试题分析:此题比较综合,要多方面考虑,
①因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;
②可利用∠ACB和∠ADB的正切求出AB;
③因为△ABD∽△EFD可利用,求出AB;
④无法求出A,B间距离.
故共有3组可以求出A,B间距离.
故选C.
C
【解析】试题分析:此题比较综合,要多方面考虑,
①因为知道∠ACB和BC的长,所以可利用∠ACB的正切来求AB的长;
②可利用∠ACB和∠ADB的正切求出AB;
③因为△ABD∽△EFD可利用,求出AB;
④无法求出A,B间距离.
故共有3组可以求出A,B间距离.
故选C. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
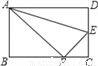
A. 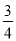 B.
B. 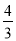 C.
C. 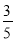 D.
D. 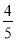
 A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A.
A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A. 如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则tanC等于( )
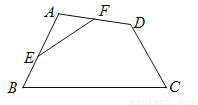
A.  B.
B.  C.
C.  D.
D. 
 B
【解析】试题分析:连接BD.
∵E、F分別是AB、AD的中点.
∴BD=2EF=4
∵BC=5,CD=3
∴△BCD是直角三角形.
∴tanC==
故选B.
B
【解析】试题分析:连接BD.
∵E、F分別是AB、AD的中点.
∴BD=2EF=4
∵BC=5,CD=3
∴△BCD是直角三角形.
∴tanC==
故选B. 如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
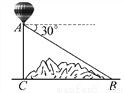
A. 100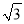 m B. 50
m B. 50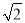 m C. 50
m C. 50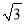 m D.
m D. 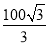 m
m
 A
【解析】试题分析:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC=(m).
故选A.
A
【解析】试题分析:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC=(m).
故选A. 等腰三角形一腰上的高与腰长之比是1?2,则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
 D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D.
D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
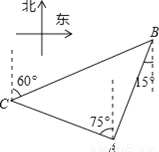
A. 20海里 B. 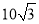 海里 C. 20
海里 C. 20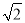 海里 D. 30海里
海里 D. 30海里
 C
【解析】∵∠ABE=15°,AD∥BE,
∴∠DAB=∠ABE=15°,
∴∠CAB=∠CAD+∠DAB=90°.
∵∠FCB=60°,CF∥BE,
∴∠CBE=∠FCB=60°.
又∠CBA+∠ABE=∠CBE,
∴∠CBA=45°.
在Rt△ABC中,
,
解得海里.
故选C.
C
【解析】∵∠ABE=15°,AD∥BE,
∴∠DAB=∠ABE=15°,
∴∠CAB=∠CAD+∠DAB=90°.
∵∠FCB=60°,CF∥BE,
∴∠CBE=∠FCB=60°.
又∠CBA+∠ABE=∠CBE,
∴∠CBA=45°.
在Rt△ABC中,
,
解得海里.
故选C. 在△ABC中,∠C=90°,AB=13,BC=5,则tanB=________.
 【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: .
【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: . 计算:(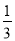 )-1-|-2+
)-1-|-2+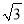 tan45°|+(
tan45°|+(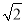 -1.41)0=________.
-1.41)0=________.
 2+
【解析】原式=3-|-2+|+1=4-2+=2+,
故答案为:2+.
2+
【解析】原式=3-|-2+|+1=4-2+=2+,
故答案为:2+. 如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC对称,若DM=1,则tan∠ADN=________.
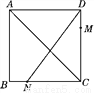
 【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===.
【解析】试题分析:在正方形ABCD中,AB=CD.由M、N两点关于对角线AC对称,所以DM=BN=1, 再由题意可知tan∠AND===tan(90°-∠CDN),进而求出CN=BC-BN=4-1=3.再由题意可知tan∠AND=tan(90°-∠CDN)===. 已知锐角A的正弦sin A是一元二次方程2x2-7x+3=0的根,则sin A=________.
 【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: .
【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: .