题目内容
如图，正方形ABCD的边长为4，点M在边DC上，M，N两点关于对角线AC对称，若DM＝1，则tan∠ADN＝________．
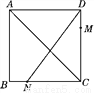
【解析】试题分析：在正方形ABCD中，AB=CD．由M、N两点关于对角线AC对称，所以DM=BN=1， 再由题意可知tan∠AND===tan（90°-∠CDN），进而求出CN=BC-BN=4-1=3．再由题意可知tan∠AND=tan（90°-∠CDN）===．
在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.
126或66
【解析】试题分析：此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．
【解析】
当∠B为锐角时（如图1），
在Rt△ABD中，
BD===5cm，
在Rt△ADC中，
CD===16cm，
∴BC=21，
∴S△ABC==×21×12=126cm2；
当∠B为钝角... 如图所示，△ABC是不等边三角形，DE=BC，以D、E为两个顶点作位置不同的三角形，使所作三角形与△ABC全等，这样的三角形最多可以画出（ ）个．
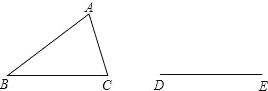
A．2 B．4 C．6 D．8
B.
【解析】
试题分析：可以做4个，分别是以D为圆心，AB为半径，作圆，以E为圆心，AC为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．然后以D为圆心，AC为半径，作圆，以E为圆心，AB为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．如图.
故选：B. 关于x的方程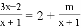
无解，则m的值为（ ）
A. ﹣5 B. ﹣8 C. ﹣2 D. 5
A
【解析】试题分析：去分母得：3x﹣2=2x+2+m，由分式方程无解，得到x+1=0，即x=﹣1，代入整式方程得：﹣5=﹣2+2+m，解得：m=﹣5，故选A． 一次函数的图象经过点(tan 45°，tan 60°)和(－cos 60°，－6tan 30°)，则此一次函数的表达式为________．
y＝2x－
【解析】tan 45°＝1，tan 60°＝，－cos 60°＝－，－6tan 30°＝－2，
设y＝kx＋b的图象经过点(1， )，（－ ，-2），
则有，解得： ，
∴一次函数解析式为： ，
故答案为： . 如图，某地修建高速公路，要从B地向C地修一座隧道(B、C在同一水平面上)，为了测量B、C两地之间的距离，某工程师乘坐热气球从C地出发，垂直上升100m到达A处，在A处观察B地的俯角为30°，则B、C两地之间的距离为( )
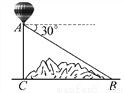
A. 100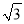
m B. 50
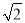m C. 50
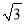m D. 
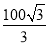m
A
【解析】试题分析：根据题意得：∠ABC=30°，AC⊥BC，AC=100m，
在Rt△ABC中，BC=（m）．
故选A． 在Rt△ABC中，∠C＝90°，AC＝2，BC＝3，那么下列各式中，正确的是( )
A. sin B＝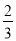
B. cos B＝
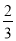C. tan B＝
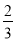D. tan B＝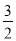
C
【解析】∵∠C＝90°，AC＝2，BC＝3，∴AB= ，
∴sinB= ，cosB=，tanB=，
故选C. 菱形以特殊的对称美而深受人们的喜爱，在生产生活中有着广泛的应用，小龙家里有一面长4.2m、宽2.8m的墙壁准备装修，现有如图甲所示的型号瓷砖，其形状是一块长30cm、宽20cm的矩形，中间白色部分为菱形，阴影部分为带淡蓝色花纹的全等的四个直角三角形，解答下列各问：
（1）小龙家里的墙壁最少要贴这种瓷砖多少块？
（2）全部贴满后，这面墙壁上有多少个有淡蓝色花纹的菱形？
(1)196;(2)169
【解析】试题分析：（1）根据墙壁的长与宽以及矩形瓷砖的长与宽进行计算求出所需要贴的瓷砖的行数与列数，然后进行计算即可得解；
（2）根据（1）中结论即可求出淡蓝色花纹的菱形个数．
试题解析：
【解析】
（1）4.2m＝420cm，2.8m＝280cm，
∵420÷30＝14，280÷20＝14，
∴贴满墙壁需要14行14列瓷砖，
... 文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
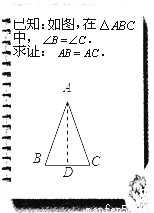
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
（1）作辅助线不能同时满足两个条件；（2）证明见解析.
【解析】试题分析：（1）线段BC的中垂线可以直接作出的，不需要附带“过点A作”；
（2）根据已知条件利用AAS可证△ABD≌△ACD，得出AB=AC．
试题解析：（1）作辅助线不能同时满足两个条件；
（2）证明：作△ABC的角平分线AD．
∴∠BAD=∠CAD，
在△ABD与△ACD中，
∴△ABD≌...