题目内容
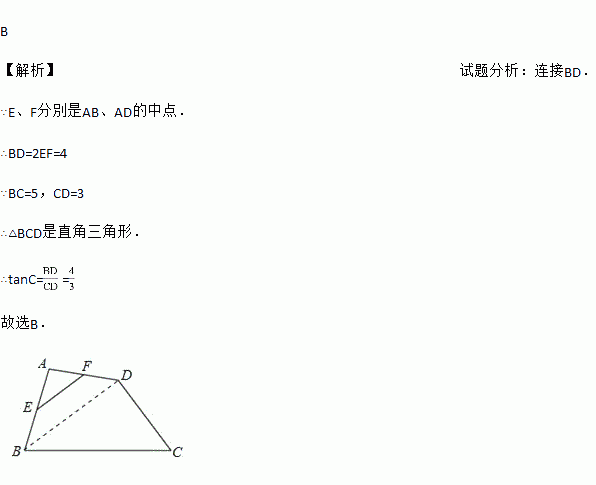
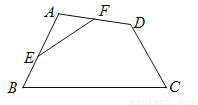
如图，在四边形ABCD中，E、F分别是AB、AD的中点．若EF=2，BC=5，CD=3，则tanC等于（ ）
A. 
B. 
C. 
D. 
B
【解析】试题分析：连接BD．
∵E、F分別是AB、AD的中点．
∴BD=2EF=4
∵BC=5，CD=3
∴△BCD是直角三角形．
∴tanC==
故选B．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
下列说法正确的是（ ）
A. 每个命题都有逆命题 B. 每个定理都有逆定理
C. 真命题的逆命题都是真命题 D. 假命题的逆命题都是假命题
A
【解析】命题由题设和结论两部分组成，所以所有的命题都有逆命题，但是所有的定理不一定有逆定理，真命题的逆命题不一定是真命题，真命题的逆命题不一定是假命题．
【解析】
A、每个命题都有逆命题，故本选项正确．
B、每个定理不一定都有逆定理，故本选项错误．
C、真命题的逆命题不一定是真命题，故本选项错误．
D、真命题的逆命题不一定是假命题，故本选项错误．
故选A． 2cos30°的值等于
（A）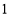
（B）
（C）
（D）
D．
【解析】
试题分析：根据特殊角的三角函数值直接解答即可．
试题解析：2cos30°=2×．
故选D． 计算：
(1) 
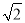(2cos 45°－sin 60°)＋
；
(2)sin 60°·cos 60°－tan 30°·tan 60°＋sin245°＋cos245°.
（1）2；（2）
【解析】试题分析：（1）先将特殊角的三角函数值代入，对最后一项的二次根式进行化简，然后再按运算顺序进行计算即可；
（2）将特殊角的三角函数值代入，按运算顺序进行计算即可得.
试题解析：（1）原式＝＝2；
（2）原式＝. 计算：(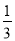
)-1－|－2＋
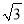tan45°|＋(
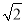－1.41)0＝________.
2＋
【解析】原式＝3－|－2＋|＋1＝4－2＋＝2＋，
故答案为：2+. 在Rt△ABC中，∠C＝90°，tan B＝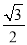
，BC＝2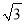
，则AC等于( )
A. 3 B. 4 C. 4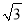
D. 6
A
【解析】∵∠C=90°，
∴tan B＝，
∴AC＝BCtan B＝2＝3，
故选A. －3x2＋2x－1＝____________＝－3x2＋_________.
－(3x2－2x＋1) (2x－1)
【解析】根据提公因式的要求，先提取负号，可得－(3x2－2x＋1)，再把2x-1看做一个整体去括号即可得（2x-1）.
故答案为：－(3x2－2x＋1) ，(2x－1). 如图所示，△EFG是由△ABC沿水平方向平移得到的，如果∠ABC＝90°，AB=3 cm，BC＝2 cm，则EF＝_________，FG=_________，EG＝_________．
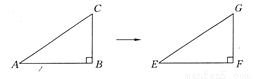
3 cm 2 cm cm
【解析】试题分析：在Rt△ABC中，AC＝＝＝（cm），
∵△EFG是由△ABC沿水平方向平移得到的，
∴EF＝AB＝3cm，FG＝BC＝2cm，EG＝AC＝cm．
故答案为3cm，2cm， cm． 在等腰梯形ABCD中，∠ABC＝2∠ACB，BD平分∠ABC，AD∥BC，如图所示，则图中的等腰三角形有( )
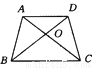
A. 1个 B. 2个 C. 3个 D. 4个
D
【解析】∵AD∥BC，∠ADB=30°，
∴∠CBD=∠ADB=30°.
∵ABCD为等腰梯形，
∴∠ABC=∠DCB=60°，则∠BAD=∠ABC-∠CBD=30°，
∴△ABD为等腰三角形.
同理可证△ACD为等腰三角形，
∵∠ABO=∠DCO=30°，∠AOB=∠DOC，AB=CD，
∴△AOB≌△DOC，
∴AO=DO，BO=CO，...