题目内容
等腰三角形一腰上的高与腰长之比是1?2,则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
 D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D.
D
【解析】如图1,当高BD在三角形的内部时,
∵高BD是腰长AB的一半,
∴sin A=,∴∠A=30°;
如图2,当高CD在三角形的外部时,
∵高CD是腰长AC的一半,
∴sin∠1=,∴∠1=30°,
∴∠BAC=180°-30°=150°,
∴该三角形的顶角的度数是30°或150°,
故选D.
练习册系列答案
相关题目
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )
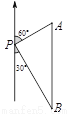
A. 60海里 B. 45海里 C. 20 海里 D. 30
海里 D. 30 海里
海里
 D
【解析】试题分析:根据条件易知△APB是直角三角形,AP=30,∠A=60°,∠B=30°,运用三角函数定义易求BP.
D
【解析】试题分析:根据条件易知△APB是直角三角形,AP=30,∠A=60°,∠B=30°,运用三角函数定义易求BP. 如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是( )

A. 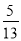 B.
B. 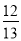 C.
C. 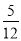 D.
D. 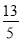
 A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B.
A
【解析】【解析】
在Rt△ABC中,由勾股定理得,BC==12,∴sinA=,故选B. 如图,已知?ABCD,点E是BC边上的一点,将边AD延长至点F,使∠AFC=∠DEC.

(1)求证:四边形DECF是平行四边形;
(2)若AB=13,DF=14,tan A=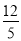 ,求CF的长.
,求CF的长.
 (1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边...
(1)见解析;(2)15
【解析】 试题分析:(1)由已知可知AD∥BC,从而得∠ADE=∠DEC,再根据∠AFC=∠DEC,从而得∠AFC=∠ADE,继而得DE∥FC,问题得证;
(2)过点D作DH⊥BC于点H,由已知得到∠BCD=∠A,AB=CD=13,再根据tan A=tan∠DCH=,从而得到DH、CH的长,从而得到CE、DE的长,继而得CF的长.
试题解析:(1)∵四边... 已知锐角A的正弦sin A是一元二次方程2x2-7x+3=0的根,则sin A=________.
 【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: .
【解析】2x2-7x+3=0,
(2x-1)(x-3)=0,
∴,
∵sinA<1,
∴sinA=,
故答案为: . 如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos ∠DCA=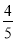 ,BC=10,则AB的值是( )
,BC=10,则AB的值是( )

A. 3 B. 6 C. 8 D. 9
 B
【解析】∵AD∥BC,∴∠DAC=∠ACB.∵AD=CD,
∴∠DAC=∠DCA.∴∠ACB=∠DCA.
∴,即,∴AC=8,
∴.
B
【解析】∵AD∥BC,∴∠DAC=∠ACB.∵AD=CD,
∴∠DAC=∠DCA.∴∠ACB=∠DCA.
∴,即,∴AC=8,
∴. 分解因式:2a2b-5ab2
 ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b).
ab(2a-5b)
【解析】试题分析:根据提公因式法分解因式,先确定公因式ab,再提取公因式即可.
试题解析:2a2b-5ab2= ab(2a-5b). 如图所示,AD∥BC,∠ABC=80°,∠BCD=50°,利用平移的知识讨论BC与AD+AB的数量关系.
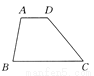
 BC=AD+AB.
【解析】试题分析:把AB平移至DE的位置,由平移的性质可得:AB=DE,AD=BE,∠DEC=∠ABC=80°,在△DEC中利用三角形的内角和定理可得∠CDE=∠BCD=50°,再由等角对等边得出DE=EC,等量代换即可得出结论.
试题解析:
【解析】
由于AD∥BC,
所以可平移AB到DE的位置(即过D点作DE∥AB交BC于点E),
则AB=D...
BC=AD+AB.
【解析】试题分析:把AB平移至DE的位置,由平移的性质可得:AB=DE,AD=BE,∠DEC=∠ABC=80°,在△DEC中利用三角形的内角和定理可得∠CDE=∠BCD=50°,再由等角对等边得出DE=EC,等量代换即可得出结论.
试题解析:
【解析】
由于AD∥BC,
所以可平移AB到DE的位置(即过D点作DE∥AB交BC于点E),
则AB=D... 下面几种三角形:
①有两个角为60°的三角形;
②三个外角都相等的三角形;
③一条边上的高也是这条边上的中线的三角形;
④有一个角为60°的等腰三角形.
其中是等边三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
 B
【解析】对于①,有两个角为60°的三角形为等边三角形,故①正确;
对于②,三个外角都相等的三角形为等边三角形,故②正确;
对于③,一条边上的高也是这条边上的中线的三角形有可能是等腰三角形或等边三角形,故③错误;
对于④,有一个角为60° 的等腰三角形为等边三角形,故④正确.
综上,①②④所述为等边三角形.
故选B.
B
【解析】对于①,有两个角为60°的三角形为等边三角形,故①正确;
对于②,三个外角都相等的三角形为等边三角形,故②正确;
对于③,一条边上的高也是这条边上的中线的三角形有可能是等腰三角形或等边三角形,故③错误;
对于④,有一个角为60° 的等腰三角形为等边三角形,故④正确.
综上,①②④所述为等边三角形.
故选B. 
