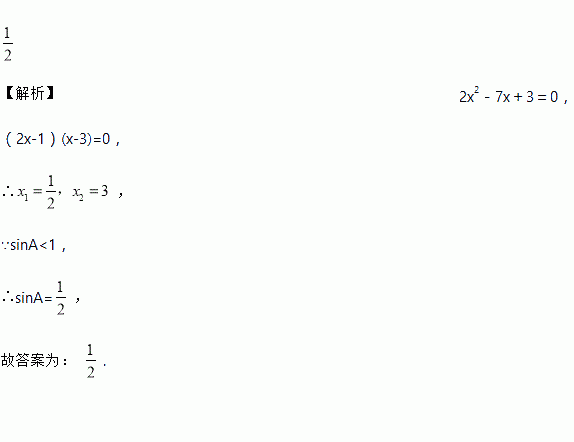题目内容
已知锐角A的正弦sin A是一元二次方程2x2－7x＋3＝0的根，则sin A＝________．
【解析】2x2－7x＋3＝0，
（2x-1）(x-3)=0，
∴，
∵sinA<1，
∴sinA=，
故答案为： .
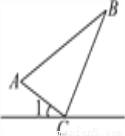
（10分）如图所示，某公路一侧有A、B两个送奶站，C为公路上一供奶站，CA和CB为供奶路线，现已测得AC＝8km，BC＝15km，AB＝17km，∠1＝30°，若有一人从C处出发，沿公路边向右行走，速度为2.5km/h，问：多长时间后这个人距B送奶站最近？
3h.
【解析】试题分析：首先根据勾股定理逆定可证明△ABC是直角三角形，然后计算出∠BCD的度数，再根据直角三角形的性质算出DC的长，然后根据速度和路程可计算出多长时间后这人距离B送奶站最近．
试题解析：【解析】
过B作BD⊥公路于D．∵82+152=172，∴AC2+BC2=AB2，∴△ABC是直角三角形，且∠ACB=90°．
∵∠1=30°，∴∠BCD=180°-90°-... 如图所示，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB＝2，则PP′＝_______.
【解析】【解析】
∵四边形ABCD为正方形，∴∠ABC=90°．∵△ABP绕点B顺时针方向旋转能与△CBP′重合，∴∠PBP′=∠ABC=90°，PB=P′B=2，∴△PBP′为等腰直角三角形，∴PP′=PB=．
故答案为： ． 分式方程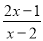
=1的解为（ ）
A. x=﹣1 B. x=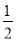
C. x=1 D. x=2
A
【解析】【解析】
去分母得：2x﹣1=x﹣2，
解得：x=﹣1，
经检验x=﹣1是分式方程的解，
则分式方程的解为x=﹣1．
故选：A． 计算：
(1) 
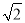(2cos 45°－sin 60°)＋
；
(2)sin 60°·cos 60°－tan 30°·tan 60°＋sin245°＋cos245°.
（1）2；（2）
【解析】试题分析：（1）先将特殊角的三角函数值代入，对最后一项的二次根式进行化简，然后再按运算顺序进行计算即可；
（2）将特殊角的三角函数值代入，按运算顺序进行计算即可得.
试题解析：（1）原式＝＝2；
（2）原式＝. 等腰三角形一腰上的高与腰长之比是1?2，则等腰三角形顶角的度数为( )
A. 30° B. 50° C. 60°或120° D. 30°或150°
D
【解析】如图1，当高BD在三角形的内部时，
∵高BD是腰长AB的一半，
∴sin A＝，∴∠A＝30°；
如图2，当高CD在三角形的外部时，
∵高CD是腰长AC的一半，
∴sin∠1＝，∴∠1＝30°，
∴∠BAC=180°-30°=150°，
∴该三角形的顶角的度数是30°或150°，
故选D． 在Rt△ABC中，∠C＝90°，tan B＝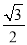
，BC＝2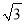
，则AC等于( )
A. 3 B. 4 C. 4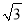
D. 6
A
【解析】∵∠C=90°，
∴tan B＝，
∴AC＝BCtan B＝2＝3，
故选A. 在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形．依照图中标注的数据，请你计算空白部分的面积．
ab – ac – bc ＋ c2
【解析】试题分析：把②向左平移c，④向上平移c，③先向上平移c，再向左平移c，使①②③④拼成一个长为(a－c)，宽为(b－c)的矩形，然后根据矩形的面积公式进行计算即可．
试题解析：
如图，将四块空白部分向①拼拢（即平移），这样就形成了一个长为(a－c)，宽为(b－c)的矩形．
∴S空白＝(a－c)×(b－c)＝ab – ac – bc ... 四边形ABCD是正方形．
(1)如图(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；
(2)在(1)中，线段EF与AF，BF的等量关系是____；(不需证明，直接写出结论即可)
(3)如图(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是____，线段EF与AF，BF的等量关系是____．(不需证明，直接写出结论即可)
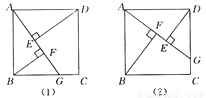
EF＝AF－BF △ABF≌△DAE EF＝BF－AF
【解析】试题分析：（1）根据正方形的性质可知：△ABF≌△ADE；
（2）利用全等三角形的性质，AE=BF，AF=DE，得出AF-BF=EF；
（3）同理可得出图（2），△ABF≌△DAE，EF=BF-AF．
(1) 证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，
∴∠BAF+∠DAE＝90°．
...