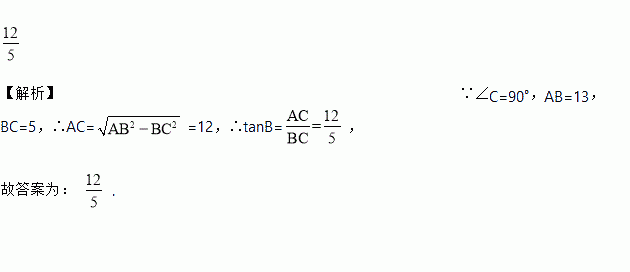题目内容
在△ABC中,∠C=90°,AB=13,BC=5,则tanB=________.
 【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: .
【解析】∵∠C=90°,AB=13,BC=5,∴AC==12,∴tanB=,
故答案为: .
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案下列命题中,其逆命题成立的是__.(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
 ①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
...
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案。
①两直线平行,同旁内角互补,正确;
②如果两个角相等,那么它们是直角,错误;
③如果两个实数的平方相等,那么这两个实数相等,错误;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形,正确.
... 在△ABC中,若cosA=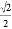 ,tanB=
,tanB=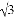 ,则这个三角形一定是( )
,则这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
 A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A.
A
【解析】试题解析:∵cosA=,tanB=,
∴∠A=45°,∠B=60°.
∴∠C=180°-45°-60°=75°.
∴△ABC为锐角三角形.
故选A. 小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm(参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).

(1)求证:AC∥BD.
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°).
(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
 (1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
∴所以:小红的连衣裙垂挂在衣架后的总...
(1)见解析;(2)61.9°;(3)会拖落到地面.
【解析】试题解析
(1)证明:证法一: 相交于点 ,
同理可证:
证法二:
∴
又
(2)【解析】
在中, 作于点,
则
用计算器求得
(3)解法一:小红的连衣裙会拖落到地面;
在中,
过点 作于点,
同可证:
则
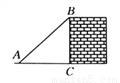
∴所以:小红的连衣裙垂挂在衣架后的总... 如图所示,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠BAC=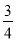 ,则梯子AB的长度为______米.
,则梯子AB的长度为______米.
 4
【解析】在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米.
4
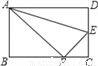
【解析】在Rt△BCA中,AC=3米,cos∠BAC=,所以AB=4米,即梯子的长度为4米. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A. 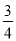 B.
B. 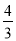 C.
C. 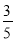 D.
D. 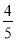
 A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A.
A
【解析】试题解析:根据题意可得:在Rt△ABF中,有AB=8,AF=AD=10,BF=6,
而Rt△ABF∽Rt△EFC,故有∠EFC=∠BAF,故tan∠EFC=tan∠BAF=.
故选A. 计算:17×3.14+61×3.14+22×3.14;
 314
【解析】试题分析:根据提公因式法分解因式,先确定公因式3.14,再提取公因式即可.
试题解析:17×3.14+61×3.14+22×3.14
=3.14×(17+61+22)
=3.14×100
=314
314
【解析】试题分析:根据提公因式法分解因式,先确定公因式3.14,再提取公因式即可.
试题解析:17×3.14+61×3.14+22×3.14
=3.14×(17+61+22)
=3.14×100
=314 如图所示,△ABC沿射线MN方向平移一定距离后成为△A′B′C′.找出两个三角形中平行且相等的线段以及全等的三角形.
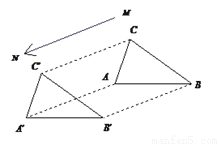
 AB、A′B′;BC、B′C′;AC、A′C′;△ABC≌△A′B′C′
【解析】试题分析:根据平移前后两个图形的对应线段平行且相等可以直接找出两个三角形中平行且相等的线段;根据平移前后的两个图形全等可知直接找出全等的三角形.
试题解析:
【解析】
两个三角形中平行且相等的线段有:AB与A’B’,BC与B’C’,AC与A’C’;
全等的三角形是:△ABC≌△A’B’C’....
AB、A′B′;BC、B′C′;AC、A′C′;△ABC≌△A′B′C′
【解析】试题分析:根据平移前后两个图形的对应线段平行且相等可以直接找出两个三角形中平行且相等的线段;根据平移前后的两个图形全等可知直接找出全等的三角形.
试题解析:
【解析】
两个三角形中平行且相等的线段有:AB与A’B’,BC与B’C’,AC与A’C’;
全等的三角形是:△ABC≌△A’B’C’.... 等腰三角形的顶角α>90°,如果过其顶角的顶点作一条直线将这个等腰三角形分 成了两个等腰三角形,那么α的度数为________.
 108°
【解析】如图,
∵AB=AC,BD=AD,AC=CD,
∴∠1=∠B,∠2=∠4,∠B=∠C,
∵∠4=∠1+∠B=2∠B=2∠C,
∴∠2=∠4=2∠C,
∵∠2+∠4+∠C=180°,
∴5∠C=180°,
∴∠C=36°,
∴α=∠BAC=180°-2∠C=108°.
108°
【解析】如图,
∵AB=AC,BD=AD,AC=CD,
∴∠1=∠B,∠2=∠4,∠B=∠C,
∵∠4=∠1+∠B=2∠B=2∠C,
∴∠2=∠4=2∠C,
∵∠2+∠4+∠C=180°,
∴5∠C=180°,
∴∠C=36°,
∴α=∠BAC=180°-2∠C=108°.