��Ŀ����
Ϊ�˲���������������A��B����֮��ľ��룬����ʵ�������������ͼ��ʾ��ͼ�Σ�����AB��BE��EF��BE��AF��BE�ڵ�D��C��BD�ϣ�����λͬѧ�ֱ����������4�����ݣ���BC����ACB����CD����ACB����ADB����EF��DE��BD����DE��DC��BC.�ܸ����������ݣ����A��B����֮��������(����)
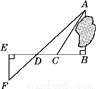
A. 1�� B. 2�� C. 3�� D. 4��
 C
���������������������Ƚ��ۺϣ�Ҫ��濼�ǣ�
����Ϊ֪����ACB��BC�ij������Կ����á�ACB����������AB�ij���
�ڿ����á�ACB�͡�ADB���������AB��
����Ϊ��ABD�ס�EFD�����ã����AB��
�������A��B����룮
�ʹ���3��������A��B����룮
��ѡC��
C
���������������������Ƚ��ۺϣ�Ҫ��濼�ǣ�
����Ϊ֪����ACB��BC�ij������Կ����á�ACB����������AB�ij���
�ڿ����á�ACB�͡�ADB���������AB��
����Ϊ��ABD�ס�EFD�����ã����AB��
�������A��B����룮
�ʹ���3��������A��B����룮
��ѡC��
���������߶��У������ֱ�������ε��ǣ�������
A. a=1��b=2��c=3 B. a=4��b=2��c=3
C. a=4��b=2��c=5 D. a=4��b=5��c=3
 D
�����������������A���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
B���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
C���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
D���ߣ����ܹ���ֱ�������Σ��ʱ�ѡ����ȷ��
��ѡD��
D
�����������������A���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
B���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
C���ߣ���ܹ���ֱ�������Σ��ʱ�ѡ�����
D���ߣ����ܹ���ֱ�������Σ��ʱ�ѡ����ȷ��
��ѡD�� ���ʽ���̣�
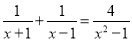
 x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�.
x��2
��������������������ս��ʽ���̵IJ���ⷽ�̼���.
���������ȥ��ĸ����
�����
�ϲ�ͬ�����
ϵ����Ϊ1����
���飺��ʱ��
��ԭ���̵Ľ�. ��ͼ����֪������ABCD�ı߳�Ϊ2��������߶�BD���ŵ�B��ת��D����CB���ӳ����ϵ�D�䴦����ôtan��BAD�䣽________.
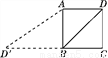
 ������������֪����ABD��=90�㣬BD=BD��==2����
��tan��BAD��==��
�ʴ�Ϊ�� .
������������֪����ABD��=90�㣬BD=BD��==2����
��tan��BAD��==��
�ʴ�Ϊ�� . ��ͼ����ij����B������һ��������ҵ���洬����ƫ��15�㷽���A�������洬�ر�ƫ��75�㷽����40����/Сʱ���ٶȺ��У����а�Сʱ��C������C���۲B��C�ı�ƫ��60�㷽���ϣ���B��C֮��ľ���Ϊ��������
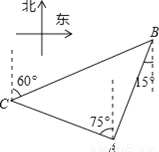
A. 20���� B. 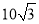 ���� C. 20
���� C. 20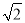 ���� D. 30����
���� D. 30����
 C
���������ߡ�ABE��15�㣬AD��BE��
���DAB����ABE��15�㣬
���CAB����CAD����DAB��90�㣮
�ߡ�FCB��60�㣬CF��BE��
���CBE����FCB��60�㣮
�֡�CBA����ABE����CBE��
���CBA��45�㣮
��Rt��ABC��
��
��ú��
��ѡC��
C
���������ߡ�ABE��15�㣬AD��BE��
���DAB����ABE��15�㣬
���CAB����CAD����DAB��90�㣮
�ߡ�FCB��60�㣬CF��BE��
���CBE����FCB��60�㣮
�֡�CBA����ABE����CBE��
���CBA��45�㣮
��Rt��ABC��
��
��ú��
��ѡC�� ���㣺20162��2016��2015.
 2016
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽ2016������ȡ����ʽ����.
���������20162��2016��2015
=2016����2016-2015��
=2016.
2016
����������������������ṫ��ʽ���ֽ���ʽ����ȷ������ʽ2016������ȡ����ʽ����.
���������20162��2016��2015
=2016����2016-2015��
=2016. ��ʽ�֡�������
x2��3x =______________.
 x(x-3)
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3����
x(x-3)
�������������������ȡ����ʽx���ɣ���x2��3x=x��x��3���� ��ͼ��ʾ����ABC����ƽ�Ƶõ���DEF����֪CE��2 cm��AC��3 cm��AB��4 cm����A��90�㣬��CF��_________cm��ƽ�Ƶľ�����_________��
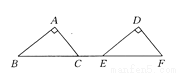
 7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
�ʴ�Ϊ��7��7cm��
7 7 cm
�������������������Rt��ABC�У��ɹ��ɶ����ã�
BC������5��cm����
�ߡ�ABC����ƽ�Ƶõ���DEF��
��EF��BC��5cm��
��CF��CE��EF��2��5��7��cm����
��C����F���Ӧ��
��ƽ�Ƶľ�����CF�ij��ȣ�
��ƽ�Ƶľ�����7cm��
�ʴ�Ϊ��7��7cm�� ����ƽ��ֻ�ı�ͼ�ε��Ƿ��棬û�иı�ͼ�ε��ļ����棿
 ����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε���״����С.
���������������������ƽ�Ƶ������ش�.
���������
����ƽ�Ƶ��������Եó�����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε� ��״����С.
����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε���״����С.
���������������������ƽ�Ƶ������ش�.
���������
����ƽ�Ƶ��������Եó�����ƽ��ֻ�ı�ͼ�ε�λ�ã�û�иı�ͼ�ε� ��״����С. 
