下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=4，b=2，c=3
C. a=4，b=2，c=5 D. a=4，b=5，c=3
D
【解析】试题分析：A．∵，∴不能构成直角三角形，故本选项错误；
B．∵，∴不能构成直角三角形，故本选项错误；
C．∵，∴不能构成直角三角形，故本选项错误；
D．∵，∴能构成直角三角形，故本选项正确．
故选D． 由下列条件不能判定△ABC是直角三角形的是( )
A. ∠A＝37°，∠C＝53° B. ∠A－∠C＝∠B
C. ∠A∶∠B∶∠C＝3∶4∶5 D. ∠A∶∠B∶∠C＝2∶3∶5
C
【解析】解：A．∠B=180°－（37°+53°）=90°，是直角三角形；
B．∠B+∠C=∠A=180°－∠A，∴∠A=90°，是直角三角形；
C．∠C=180°×=75°，不是直角三角形；
D．∠C=180°×=90°，是直角三角形．
故选C． 下列说法正确的是（ ）
A. 每个命题都有逆命题 B. 每个定理都有逆定理
C. 真命题的逆命题都是真命题 D. 假命题的逆命题都是假命题
A
【解析】命题由题设和结论两部分组成，所以所有的命题都有逆命题，但是所有的定理不一定有逆定理，真命题的逆命题不一定是真命题，真命题的逆命题不一定是假命题．
【解析】
A、每个命题都有逆命题，故本选项正确．
B、每个定理不一定都有逆定理，故本选项错误．
C、真命题的逆命题不一定是真命题，故本选项错误．
D、真命题的逆命题不一定是假命题，故本选项错误．
故选A． 如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（ ）
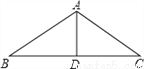
A. 5 B. 6 C. 8 D. 10
C
【解析】因为AB＝AC，AD是∠BAC的平分线，所以BC=2BD.
因为BD＝4，所以BC=2BD=2×4=8.
故选C. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B与灯塔P之间的距离为( )
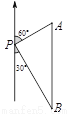
A. 60海里 B. 45海里 C. 20
海里 D. 30海里
D
【解析】试题分析：根据条件易知△APB是直角三角形，AP=30，∠A=60°，∠B=30°，运用三角函数定义易求BP． 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A. 
B. 
C. 4 D. 5
C
【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x，
∵D是BC的中点，
∴BD=3，
在Rt△BDN中，x2+32=（9－x）2，
解得x=4．
故线段BN的长为4．
故选C． 下列命题中，其逆命题成立的是__．（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形．
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题，再分析逆命题是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。
①两直线平行，同旁内角互补，正确；
②如果两个角相等，那么它们是直角，错误；
③如果两个实数的平方相等，那么这两个实数相等，错误；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形，正确．
... 已知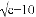
＋|a－6|＋(b－8)2＝0，则以a、b、c为三边的三角形是__________.
直角三角形
【解析】【解析】
∵，∴a-6=0， b-8=0，c-10=0，∴a=6，b=8，c=10，
∴a2+b2=c2，∴以a、b、c为三边的三角形是直角三角形．故答案为：直角． 在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.
126或66
【解析】试题分析：此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．
【解析】
当∠B为锐角时（如图1），
在Rt△ABD中，
BD===5cm，
在Rt△ADC中，
CD===16cm，
∴BC=21，
∴S△ABC==×21×12=126cm2；
当∠B为钝角... （10分）如图所示，某公路一侧有A、B两个送奶站，C为公路上一供奶站，CA和CB为供奶路线，现已测得AC＝8km，BC＝15km，AB＝17km，∠1＝30°，若有一人从C处出发，沿公路边向右行走，速度为2.5km/h，问：多长时间后这个人距B送奶站最近？
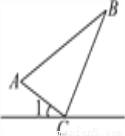
3h.
【解析】试题分析：首先根据勾股定理逆定可证明△ABC是直角三角形，然后计算出∠BCD的度数，再根据直角三角形的性质算出DC的长，然后根据速度和路程可计算出多长时间后这人距离B送奶站最近．
试题解析：【解析】
过B作BD⊥公路于D．∵82+152=172，∴AC2+BC2=AB2，∴△ABC是直角三角形，且∠ACB=90°．
∵∠1=30°，∴∠BCD=180°-90°-...