题目内容
已知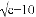
＋|a－6|＋(b－8)2＝0，则以a、b、c为三边的三角形是__________.
直角三角形
【解析】【解析】
∵，∴a-6=0， b-8=0，c-10=0，∴a=6，b=8，c=10，
∴a2+b2=c2，∴以a、b、c为三边的三角形是直角三角形．故答案为：直角．
练习册系列答案
相关题目
用科学记算器算得①293=24389；②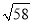
≈7.615773106；③sin35°≈0.573576436；④若tana=5，则锐角a≈0.087488663°．其中正确的是（ ）
A. ①②③ B. ①②④ C. ②③④ D. ①③④
A
【解析】试题分析：①②③利用计算器计算可得是正确的，
④tan45°=1，tana=5，说明α的度数应大于45°，所以错误，
故选A． 根据已知条件写出相应不等式．
(1)－3，－2，－1,0,1都是不等式的解；
(2)不等式的负整数解只有－1，－2，－3；
(3)不等式的解的最大的值是0.
见解析
【解析】分析：根据题中的条件，得出每个小题中的数据在不等式的解集范围内即可.
本题解析：
(1)∵不等式有五个连续的整数解，
∴求不等式x-1≤0的五个最大整数解。
(2)∵不等式有三个连续的负整数解
∴求不等式2(x+1) ≤0的三个最大负整数解。
(3)∵不等式的解的最大的值是0，
∴求不等式x-1<0的最大整数解。 2a与3a的大小关系（ ）
A、2a＜3a B、2a＞3a C、2a＝3a D、不能确定
D
【解析】
试题分析：题目中没有明确a的正负，故要分情况讨论.
当时，；当时，；当时，，
故选D. 如果m＜n＜0，那么下列结论中错误的是（ ）
A、m－9＜n－9 B、－m＞－n C、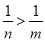
D、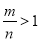
C
【解析】
试题分析：根据不等式的基本性质依次分析各项即可.
m＜n＜0，
∴m－9＜n－9，－m＞－n，，，
故选C. 下列说法正确的是（ ）
A. 每个命题都有逆命题 B. 每个定理都有逆定理
C. 真命题的逆命题都是真命题 D. 假命题的逆命题都是假命题
A
【解析】命题由题设和结论两部分组成，所以所有的命题都有逆命题，但是所有的定理不一定有逆定理，真命题的逆命题不一定是真命题，真命题的逆命题不一定是假命题．
【解析】
A、每个命题都有逆命题，故本选项正确．
B、每个定理不一定都有逆定理，故本选项错误．
C、真命题的逆命题不一定是真命题，故本选项错误．
D、真命题的逆命题不一定是假命题，故本选项错误．
故选A． 如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
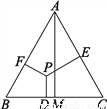
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=... 请你用所学的知识，在下面两项中任选其一作图．
（1）参考下图，为班级的黑板报设计一组花边图案．
（2）以三角形、矩形、圆形为“基本图案”通过平移、旋转、轴对称为班级设计一个班徽．
见解析
【解析】试题分析：本题主要考查大家根据轴对称性质设计花边图案的能力，而且要符合考题中的四点要求，这是一道融数学与美术为一体的综合创新素质题
试题解析：【解析】
选（1）．如图：设计花边图案为： 计算：(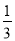
)-1－|－2＋
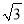tan45°|＋(
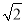－1.41)0＝________.
2＋
【解析】原式＝3－|－2＋|＋1＝4－2＋＝2＋，
故答案为：2+.