题目内容
下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=4，b=2，c=3
C. a=4，b=2，c=5 D. a=4，b=5，c=3
D
【解析】试题分析：A．∵，∴不能构成直角三角形，故本选项错误；
B．∵，∴不能构成直角三角形，故本选项错误；
C．∵，∴不能构成直角三角形，故本选项错误；
D．∵，∴能构成直角三角形，故本选项正确．
故选D．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
下面四个数中，最大的是（ ）
A.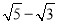 
B. sin88° C. tan46° D.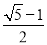 
C
【解析】试题分析：A、≈2.236-1.732≈0.504；
B、sin88°≈0.999；
C、tan46°≈1.036；
D、 ≈ ≈0.568．
故tan46°最大，
故选：C． 若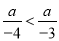
，试判断a的正负性．
a为负数
【解析】分析：先根据不等式基本性质3,两边都乘以,再根据不等式基本性质1,两边都减去3a即可得出结论.
本题解析：根据不等式基本性质3，两边都乘以－12，得3a＞4a．
根据不等式基本性质1，两边都减去3a，得0＞a ，即a<0 ，即a为负数． 如果m＜n＜0，那么下列结论中错误的是（ ）
A、m－9＜n－9 B、－m＞－n C、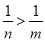
D、
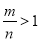
C
【解析】
试题分析：根据不等式的基本性质依次分析各项即可.
m＜n＜0，
∴m－9＜n－9，－m＞－n，，，
故选C. 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A. 
B. 
C. 4 D. 5
C
【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x，
∵D是BC的中点，
∴BD=3，
在Rt△BDN中，x2+32=（9－x）2，
解得x=4．
故线段BN的长为4．
故选C． 如图，在等边△ABC中，P为△ABC内任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，AM⊥BC于M，试猜想AM、PD、PE、PF之间的关系，并说明你的猜想．
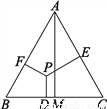
AM＝PD＋PE＋PF，理由见解析
【解析】试题分析：连接AP、BP、CP，根据面积相等，又利用△ABC是等边三角形，即可得PE+PD+PF=AM.
试题解析：PE+PD+PF=AM，理轴如下：
连接AP、BP、CP，
∵S△ABP+S△BCP+S△ACP=S△ABC，
∴AB×PE+BC×PD+AC×PF＝BC×AM，
∵△ABC是等边三角形，
∴AB=... 已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C... 我国国旗上的四个小五角星，通过_______________移动可以相互得到．
旋转或旋转和平移
【解析】【解析】
四个小五角星通过旋转可以互相得到．故答案为：旋转． 为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE，EF⊥BE，AF交BE于点D，C在BD上．有四位同学分别测量出以下4组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B两点之间距离的有( )
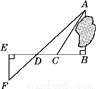
A. 1组 B. 2组 C. 3组 D. 4组
C
【解析】试题分析：此题比较综合，要多方面考虑，
①因为知道∠ACB和BC的长，所以可利用∠ACB的正切来求AB的长；
②可利用∠ACB和∠ADB的正切求出AB；
③因为△ABD∽△EFD可利用，求出AB；
④无法求出A，B间距离．
故共有3组可以求出A，B间距离．
故选C．