题目内容
下列命题中，其逆命题成立的是__．（只填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形．
①④
【解析】把一个命题的条件和结论互换就得到它的逆命题，再分析逆命题是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案。
①两直线平行，同旁内角互补，正确；
②如果两个角相等，那么它们是直角，错误；
③如果两个实数的平方相等，那么这两个实数相等，错误；
④如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形，正确．
...
考前必练系列答案Rt△ABC中，∠C=90°，a：b=3：4，运用计算器计算，∠A的度数（精确到1°）（ ）
A. 30° B. 37° C. 38° D. 39°
B
【解析】试题分析：tanA===0.75，
运用计算器可得：∠A=37°．
故选B． 不等式3x＜6的解集是_____；使该不等式成立的正整数解是___，当_____时，不等式3x＞7不成立．
x＜2 1 x≤
【解析】3x＜6的解集为x<2；
其正整数解为1，
当x≤时，不等式3x＞7不成立.
故答案为(1). x＜2 (2). 1 (3). x≤ 有下列说法：
（1）若a＜b，则－a＞－b； （2）若xy＜0，则x＜0，y＜0；
（3）若x＜0，y＜0，则xy＜0； （4）若a＜b，则2a＜a＋b；
（5）若a＜b，则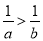
； （6）若
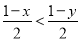，则x＞y.
其中正确的说法有（ ）
A、2个 B、3个 C、4个 D、5个
B
【解析】
试题分析：根据不等式的基本性质依次分析各项即可。
（1）若a＜b，则－a＞－b，正确；
（2）若xy＜0，则x＜0，y＞0或x＞0，y＜0，错误；
（3）若x＜0，y＜0，则xy＞0，错误；
（4）若a＜b，则2a＜a＋b，正确；
（5）若a＜0＜b，则，错误；
（6）若，则x＞y，正确.
故选B. 如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．
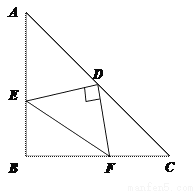
连结BD，证△BED≌△CFD和△AED≌△BFD，得BF=4，BE=3，再运用勾股定理求得EF=5 由下列条件不能判定△ABC是直角三角形的是( )
A. ∠A＝37°，∠C＝53° B. ∠A－∠C＝∠B
C. ∠A∶∠B∶∠C＝3∶4∶5 D. ∠A∶∠B∶∠C＝2∶3∶5
C
【解析】解：A．∠B=180°－（37°+53°）=90°，是直角三角形；
B．∠B+∠C=∠A=180°－∠A，∴∠A=90°，是直角三角形；
C．∠C=180°×=75°，不是直角三角形；
D．∠C=180°×=90°，是直角三角形．
故选C． 如图，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，直线AD交EF于点O.问直线AD是线段EF的垂直平分线吗？请说明理由．
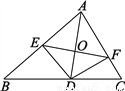
AD是线段EF的垂直平分线，理由见解析
【解析】试题分析：由AD为△ABC的角平分线，得到DE=DF，推出∠AEF和∠AFE相等，得到AE=AF，即可推出结论.
试题解析：∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠AED=∠AFD=90°，
∴∠DEF=∠DFE，
∴∠AEF=∠AFE，
∴AE=AF，
∴点A、D都在EF的垂直... 请充分发挥你的想象力，任选其一完成下面的设计
（1）以一直角三角形为“基本图形”，利用旋转而得到一个风车或风轮图案．你能设计出几种风车风轮图案呢？请将你的图案画出来，完成后与同学进行交流．
（2）利用圆、三角形、正六边形，通过平移或旋转来设计一个图案，完成后与同学交流你的作品，说明你的设计意图．
见解析
【解析】试题分析：根据旋转的角度不同可得到不同的风车形状，只要满足题意即可．
试题解析：【解析】
选（1），所画的是旋转90°的情况． 在△ABC中，∠C＝90°，AB＝13，BC＝5，则tanB＝________．
【解析】∵∠C=90°，AB=13，BC=5，∴AC==12，∴tanB=，
故答案为： .