��Ŀ����
��ͼ��һ���ִ�λ�ڵ���P�ı�ƫ��60�㷽�������P�ľ���Ϊ30�����A�����ִ������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��30�㷽���ϵ�B�������ʱ�ִ�����λ��B�����P֮��ľ���Ϊ( )
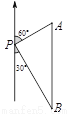
A. 60���� B. 45���� C. 20 ���� D. 30
���� D. 30 ����
����
 D
���������������������������֪��APB��ֱ�������Σ�AP=30����A=60�㣬��B=30�㣬�������Ǻ�����������BP��
D
���������������������������֪��APB��ֱ�������Σ�AP=30����A=60�㣬��B=30�㣬�������Ǻ�����������BP��
����sin20�㣭cos20���ֵ��(��ȷ��0.000 1)( )
A. ��0.597 6 B. 0.597 6
C. ��0.597 7 D. 0.597 7
 C
����������MODE�����֣�DEG����sin20?cos20=����ʾ��?0.5977.
��ѡ��C.
C
����������MODE�����֣�DEG����sin20?cos20=����ʾ��?0.5977.
��ѡ��C. ����ʽx��3��1�Ľ⼯��( )
A. x��2 B. x��4 C. x����2 D. x����4
 B
��������������������ݲ���ʽ�Ļ������ʼ��ɵõ����.
x��3��1
x��4
��ѡB.
B
��������������������ݲ���ʽ�Ļ������ʼ��ɵõ����.
x��3��1
x��4
��ѡB. ���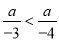 ����a�������㣨 ��
����a�������㣨 ��
A��a��0 B��a��0 C��a��0 D��a������
 C
��������
������������ݲ���ʽ�Ļ������ʼ����ж�.
��
��a��0��
��ѡC.
C
��������
������������ݲ���ʽ�Ļ������ʼ����ж�.
��
��a��0��
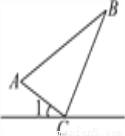
��ѡC. ��10�֣���ͼ��ʾ��ij��·һ����A��B��������վ��CΪ��·��һ����վ��CA��CBΪ����·�ߣ����Ѳ��AC��8km��BC��15km��AB��17km����1��30�㣬����һ�˴�C���������ع�·���������ߣ��ٶ�Ϊ2.5km/h���ʣ��ʱ�������˾�B����վ�����
 3h.
��������������������ȸ��ݹ��ɶ����涨��֤����ABC��ֱ�������Σ�Ȼ��������BCD�Ķ������ٸ���ֱ�������ε��������DC�ij���Ȼ������ٶȺ�·�̿ɼ�����ʱ������˾���B����վ�����
�����������������
��B��BD��·��D����82+152=172����AC2+BC2=AB2�����ABC��ֱ�������Σ��ҡ�ACB=90�㣮
�ߡ�1=30�㣬���BCD=180��-90��-...
3h.
��������������������ȸ��ݹ��ɶ����涨��֤����ABC��ֱ�������Σ�Ȼ��������BCD�Ķ������ٸ���ֱ�������ε��������DC�ij���Ȼ������ٶȺ�·�̿ɼ�����ʱ������˾���B����վ�����
�����������������
��B��BD��·��D����82+152=172����AC2+BC2=AB2�����ABC��ֱ�������Σ��ҡ�ACB=90�㣮
�ߡ�1=30�㣬���BCD=180��-90��-... ��ͼ��ֱ��AB�� CD���� B=50�㣬�� C=40�㣬���E���ڣ����� ��
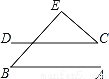
A. 70�� B. 80�� C. 90�� D. 100��
 C
���������������������ƽ���ߵ����ʵõ���1=��B=50�㣬�������ε��ڽǺͶ����ɵá�E=180�㩁��B����1=90�㣬�ʴ�ѡC��
C
���������������������ƽ���ߵ����ʵõ���1=��B=50�㣬�������ε��ڽǺͶ����ɵá�E=180�㩁��B����1=90�㣬�ʴ�ѡC�� ��ͼ���ڡ�ABC�У�AB=AD=DC����BAD=26��.���B�͡�C�Ķ���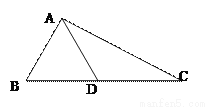
 77�� 38.5��
����������������
�� AB��AD��
���B����ADB�� ������������ 2��
���ڡ�ABD�У���B+��ADB+��BAD��180�㣬��BAD��26�㣬
���B����ADB��77�㣮 ������������ 4��
��AD.��DC��
���DAC ����C�� ������������ 6��
�ߡ�ADB����DAC+��C�� ������������ 7��
���ADB��2��C��
...
77�� 38.5��
����������������
�� AB��AD��
���B����ADB�� ������������ 2��
���ڡ�ABD�У���B+��ADB+��BAD��180�㣬��BAD��26�㣬
���B����ADB��77�㣮 ������������ 4��
��AD.��DC��
���DAC ����C�� ������������ 6��
�ߡ�ADB����DAC+��C�� ������������ 7��
���ADB��2��C��
... ������һ�ų����ε�ֽƬ�۳�һ�����������𣿶�����һ�ԣ�����������۷���
 ��ͼ���ȰѾ���ֽƬ���ۣ�Ȼ��������BM����ʹC����EF�ϵ�N�㣬���۳�BM��CN���ɣ�
������������������ѳ�����ֽƬABCD�Ŀ����ۣ�Ȼ��չ�����ۺۼ�ΪEF���ٰ�AD�����𣬵�D�۵���EF�ϣ���EF���غϵ�ΪM����CD�ϵ��ۺ�Ϊ��G������GM���ۣ���AB�ϵ��ۺ�ΪH����������AHG����һ���������Σ�
�����������������
��ͼ��
����AM���ڡ�AMG�͡�AMH�У�
AM=...
��ͼ���ȰѾ���ֽƬ���ۣ�Ȼ��������BM����ʹC����EF�ϵ�N�㣬���۳�BM��CN���ɣ�
������������������ѳ�����ֽƬABCD�Ŀ����ۣ�Ȼ��չ�����ۺۼ�ΪEF���ٰ�AD�����𣬵�D�۵���EF�ϣ���EF���غϵ�ΪM����CD�ϵ��ۺ�Ϊ��G������GM���ۣ���AB�ϵ��ۺ�ΪH����������AHG����һ���������Σ�
�����������������
��ͼ��
����AM���ڡ�AMG�͡�AMH�У�
AM=... ����������һ���ϵĸ�������֮����1?2������������ζ��ǵĶ���Ϊ(����)
A. 30�� B. 50�� C. 60���120�� D. 30���150��
 D
����������ͼ1������BD�������ε��ڲ�ʱ��
�߸�BD������AB��һ�룬
��sin A�������A��30�㣻
��ͼ2������CD�������ε��ⲿʱ��
�߸�CD������AC��һ�룬
��sin��1�������1��30�㣬
���BAC=180��-30��=150�㣬
��������εĶ��ǵĶ�����30���150�㣬
��ѡD��
D
����������ͼ1������BD�������ε��ڲ�ʱ��
�߸�BD������AB��һ�룬
��sin A�������A��30�㣻
��ͼ2������CD�������ε��ⲿʱ��
�߸�CD������AC��һ�룬
��sin��1�������1��30�㣬
���BAC=180��-30��=150�㣬
��������εĶ��ǵĶ�����30���150�㣬
��ѡD�� 
