题目内容
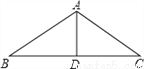
如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A. 5 B. 6 C. 8 D. 10
 C
【解析】因为AB=AC,AD是∠BAC的平分线,所以BC=2BD.
因为BD=4,所以BC=2BD=2×4=8.
故选C.
C
【解析】因为AB=AC,AD是∠BAC的平分线,所以BC=2BD.
因为BD=4,所以BC=2BD=2×4=8.
故选C.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
用计算器计算cos44°的结果(精确到0.01)是( )
A. 0.90 B. 0.72 C. 0.69 D. 0.66
 B
【解析】试题分析:用计算器解cos44°≈0.72.
故选B.
B
【解析】试题分析:用计算器解cos44°≈0.72.
故选B. 下列数值中,是不等式x-2>2的一个解的是( )
A. 0 B. 2
C. 4 D. 6
 D
【解析】解不等式x?2>2,得x>4,
而大于4的数只有6.
故选D.
D
【解析】解不等式x?2>2,得x>4,
而大于4的数只有6.
故选D. 如果t>0,那么a+t与a的大小关系是( )
A、a+t>a B、a+t<a C、a+t≥a D、不能确定
 A
【解析】
试题分析:根据不等式的基本性质即可得到结果.
t>0,
∴a+t>a,
故选A.
A
【解析】
试题分析:根据不等式的基本性质即可得到结果.
t>0,
∴a+t>a,
故选A. 在△ABC中,AB=13cm,AC=20cm,BC边上的高为12cm,则△ABC的面积为________cm2.
 126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
当∠B为钝角...
126或66
【解析】试题分析:此题分两种情况:∠B为锐角或∠B为钝角已知AB、AC的值,利用勾股定理即可求出BC的长,利用三角形的面积公式得结果.
【解析】
当∠B为锐角时(如图1),
在Rt△ABD中,
BD===5cm,
在Rt△ADC中,
CD===16cm,
∴BC=21,
∴S△ABC==×21×12=126cm2;
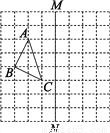
当∠B为钝角... 如图,在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)在网格上的最小正方形的边长为1,求△ABC的面积.
 (1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
(2)S△ABC=2×3-2×(×1×2)-×1×3=.
(1)见解析;(2)
【解析】试题分析:(1)根据网格特点分别找到A、B、C关于直线MN对称的点,然后顺次连接即可得;
(2)用三角形ABC所在长方形的面积减去四周三个小三角形的面积即可得.
试题解析:(1)如图所示:
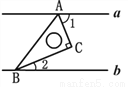
(2)S△ABC=2×3-2×(×1×2)-×1×3=. 如图所示的四个图形中,从几何图形变换的角度考虑,哪一个与其他三个不同?请指出这个图形,并简述你的理由.
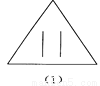
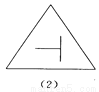
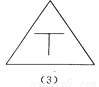
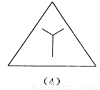
 图(2),仅它不是轴对称图形
【解析】试题分析:观察图形发现(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形,由此即可得出结论.
试题解析:【解析】
(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形.故从几何图形变换的角度考虑,图(2)与其它三个不同.
图(2),仅它不是轴对称图形
【解析】试题分析:观察图形发现(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形,由此即可得出结论.
试题解析:【解析】
(1)(3)(4)都是轴对称图形,而(2)不是轴对称图形.故从几何图形变换的角度考虑,图(2)与其它三个不同. 如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上),为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
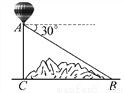
A. 100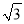 m B. 50
m B. 50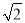 m C. 50
m C. 50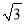 m D.
m D. 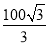 m
m
 A
【解析】试题分析:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC=(m).
故选A.
A
【解析】试题分析:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC=(m).
故选A.