题目内容
如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A. 
B. 
C. 4 D. 5
C
【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x，
∵D是BC的中点，
∴BD=3，
在Rt△BDN中，x2+32=（9－x）2，
解得x=4．
故线段BN的长为4．
故选C．
用科学记算器计算，下面结果不正确的是（ ）
A. 175=1419857
B.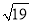 
=4.358898944
C. sin35°=0.573576436
D. 若tanα=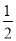
，则α=25°56′50″
D
【解析】试题分析：利用计算器分别计算后，只有D是错误的，α应等于26°33′54″．
故选D． 下列不等式中，不含有x＝－1这个解的是
A. 2x＋1≤－3 B. 2x－1≥－3
C. －2x＋1≥3 D. －2x－1≤3
A
【解析】A. ∵ 2x＋1≤－3 ，∴x≤-2，∴不含有x＝－1这个解;
B. ∵ 2x－1≥－3，∴x≥-1，∴含有x＝－1这个解
C. ∵－2x＋1≥3 ，∴x≤-1，∴含有x＝－1这个解
D. ∵－2x－1≤3，∴x≥-2，∴含有x＝－1这个解
故选A. 已知有理数a、b、c在数轴上的位置如图所示，则下列式子正确的是（ ）
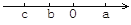
A. cb＞ab B. ac＞ab C. cb＜ab D. c＋b＞a＋b
A
【解析】试题分析：先根据数轴的特点得出a＞0＞b＞c，再根据不等式的性质进行判断：
A、∵a＞0＞b＞c，∴cb＞0＞ab. 选项正确.
B、∵c＜b，a＞0，∴ac＜ab. 选项错误.
C、∵c＜a，b＜0，∴cb＞ab. 选项错误.
D、∵c＜a，∴c+b＜a+b. 选项错误.
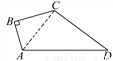
故选A． 如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：【解析】
连接AC．如图所示：
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根... 下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=4，b=2，c=3
C. a=4，b=2，c=5 D. a=4，b=5，c=3
D
【解析】试题分析：A．∵，∴不能构成直角三角形，故本选项错误；
B．∵，∴不能构成直角三角形，故本选项错误；
C．∵，∴不能构成直角三角形，故本选项错误；
D．∵，∴能构成直角三角形，故本选项正确．
故选D． 如图，在等边三角形ABC中，∠B、∠C的平分线相交于点O，作BO、CO的垂直平分线分别交BC于点E、F.小明说：“E、F是BC的三等分点．”你同意他的说法吗？请说明理由．
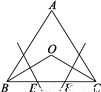
同意，理由见解析
【解析】试题分析：连接OE、OF，根据等边三角形角平分线的性质，可得∠OBC=∠OCB=30°，由BC的垂直平分线，可知BE=OE，∠EBO=∠EOB=30°，∠OEF=60°，再证，∠OFE=60°，得出△OEF为等边三角形，从而可知EF=OE=BE=OF=FC，得出结论．
试题解析：同意．理由如下：
连接OE、OF，
∵E为BO垂直平分线上的点，且∠O... 作线段AB和CD，且AB和CD互相垂直平分，交点为O，AB＝2CD．分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角星图案．将此四角星沿水平方向向右平移2厘米，作出平移前后的图形．
见解析
【解析】试题分析：根据垂直平分线的意义，画线段AB（4厘米），作AB的垂直平分线段CD（2厘米）交AB于点O，再分别取OA、OB、OC、OD的中点A′、B′、C′、D′，连结CA′、DA′、CB′、DB′、AC′、AD′、BC′、BD′得到一个四角形图案A′B′C′D′；再根据平移图形的特征，把四角形图案A′B′C′D′的四个顶点分别向右平移2厘米，再首尾连结各点，即可得到四角形图案... 如图，在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处，若渔船沿北偏西75°方向以40海里/小时的速度航行，航行半小时后到达C处，在C处观测到B在C的北偏东60°方向上，则B、C之间的距离为（ ）
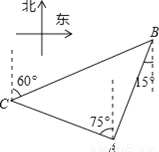
A. 20海里 B.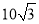 
海里 C. 20
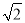海里 D. 30海里
C
【解析】∵∠ABE＝15°，AD∥BE，
∴∠DAB＝∠ABE＝15°，
∴∠CAB＝∠CAD＋∠DAB＝90°．
∵∠FCB＝60°，CF∥BE，
∴∠CBE＝∠FCB＝60°．
又∠CBA＋∠ABE＝∠CBE，
∴∠CBA＝45°．
在Rt△ABC中，
，
解得海里．
故选C．