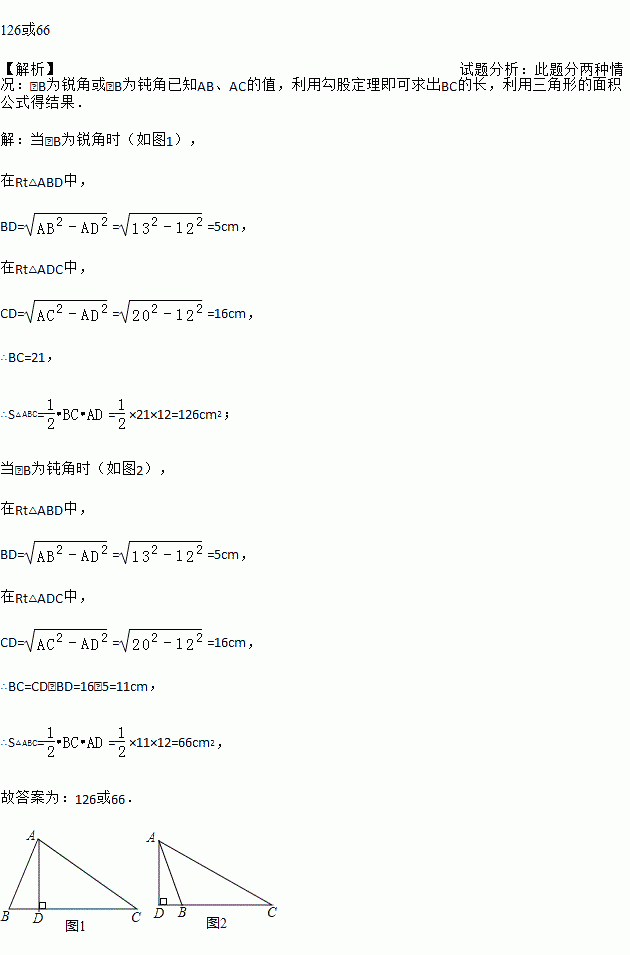题目内容
在△ABC中，AB＝13cm，AC＝20cm，BC边上的高为12cm，则△ABC的面积为________cm2.
126或66
【解析】试题分析：此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．
【解析】
当∠B为锐角时（如图1），
在Rt△ABD中，
BD===5cm，
在Rt△ADC中，
CD===16cm，
∴BC=21，
∴S△ABC==×21×12=126cm2；
当∠B为钝角...
练习册系列答案
相关题目
计算cos80°﹣sin80°的值大约为（ ）
A. 0.8111 B. ﹣0.8111 C. 0.8112
B
【解析】根据一个角的余弦等于它余角的正弦，可转化成正弦函数，根据锐角的正弦随角的度数的增大而增大，可得答案，
cos80°﹣sin80°=sin10°-sin80°<0，
观察可知只有B选项符合，
故选B. 对于解不等式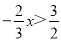
，正确的结果是（ ）
A．x＜
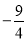B．x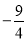＞ C．x＞-1 D．x＜-1
A．
【解析】
试题分析：先去分母得，-4x＞9，再把x的系数化为1得，x＜．
故选A． 若m＜n，比较下列各式的大小：
（1）m－3______n－3 （2）－5m______－5n （3）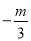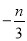
______
（4）3－m______2－n (5)0_____m－n （6）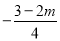
_____
< > > > > <
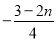
【解析】(1)m若a－b＜0，则下列各式中一定正确的是（ ）
A、a＞b B、ab＞0 C、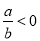
D、－a＞－b
D
【解析】
试题分析：由a－b＜0可得a＜b，再根据不等式的基本性质依次分析各项即可.
a－b＜0，
∴a＜b，
∴－a＞－b，但无法确定ab与的符号，
故选D. 如图，△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（ ）
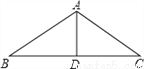
A. 5 B. 6 C. 8 D. 10
C
【解析】因为AB＝AC，AD是∠BAC的平分线，所以BC=2BD.
因为BD＝4，所以BC=2BD=2×4=8.
故选C. 如图，∠AOB＝30°，角内有一点P，PO＝10cm，两边上各有一点Q，R(均不同于点O)，则△PQR的周长的最小值是多少？
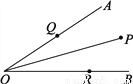
10cm
【解析】试题分析：设点P关于OA的对称点是E，关于OB的对称点是F，当点R、Q在EF上时，△PQR的周长=PQ+QR+PR=EF，此时周长最小．
试题解析：作出点P关于OA的对称点E，作出点P关于OB的对称点F，连接EF，交OA于Q，交OB于R．连接PQ，PR，PE，PF，OE，OF，
则PQ=EQ，PR=RF，
则△PQR的周长=PQ+QR+PR=EQ+QR+R... 如图，已知△ABC中，AC+BC=24，AO，BO分别是角平分线，且MN∥BA，分别交AC于N，BC于M，则△CMN的周长为（ ）
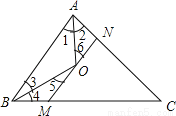
A.12 B.24 C.36 D.不确定
B
【解析】
试题分析：由AO，BO分别是角平分线求得∠1=∠2，∠3=∠4，利用平行线性质求得，∠1=∠6，∠3=∠5，利用等量代换求得∠2=∠6，∠4=∠5，即可解题．
【解析】
由AO，BO分别是角平分线得∠1=∠2，∠3=∠4，
又∵MN∥BA，∴∠1=∠6，∠3=∠5，
∴∠2=∠6，∠4=∠5，
∴AN=NO，BM=OM．
∵AC+BC=24... 如图，正方形ABCD的边长为4，点M在边DC上，M，N两点关于对角线AC对称，若DM＝1，则tan∠ADN＝________．
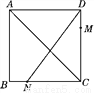
【解析】试题分析：在正方形ABCD中，AB=CD．由M、N两点关于对角线AC对称，所以DM=BN=1， 再由题意可知tan∠AND===tan（90°-∠CDN），进而求出CN=BC-BN=4-1=3．再由题意可知tan∠AND=tan（90°-∠CDN）===．