如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC交AD于点E，EF∥AC，下列结论一定成立的是( )
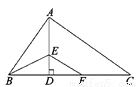
A. AB=BF B. AE=ED
C. AD=DC D. ∠ABE=∠DFE
A
【解析】【解析】
∵∠BAD+∠ABD=90°，∠ABD+∠C=90°
∴∠BAD=∠C（同角的余角相等）
又∵EF∥AC
∴∠BFE=∠C
∴∠BAD=∠BFE
又∵BE平分∠ABC
∴∠ABE=∠FBE
∴∠BEF=∠AEB，
在△ABE与△FBE中，
∠BEF=∠AEB，BE=BE，∠ABE=∠FBE
∴△ABE≌△FB... 如图，在△ABC中，CD是AB边上的高，BE是AC边的高，点O是两条高的交点，则∠A与∠1＋∠2的大小关系是( )
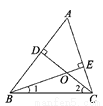
A. ∠A＞∠1＋∠2 B. ∠A=∠1＋∠2
C. ∠A＜∠1＋∠2 D. 无法确定
B
【解析】试题解析：∵CD是AB边上的高，BE是AC边上的高，
∴∠OEC=∠ADC=
又∴△ACD和△OCE中，∠ACD=∠OCE，
∴∠A=∠EOC
又∵∠EOC=∠1+∠2，
∴∠A=∠1+∠2.
故选B. 根据下列已知条件，能画出唯一△ABC的是( )
A. AB=3，BC=4，CA=8 B. AB=4，BC=3，∠A=30°
C. ∠A=60°，∠B=45°，AB=4 D. ∠C=90°，AB=6
C
【解析】由一定的已知条件画三角形，要使画出的三角形是唯一的，说明不同的人根据这些条件画出的三角形一定是全等的；而由全等三角形的判定方法可知当两个三角形满足A、B、D选项中的边、角对应相等时，两个三角形不一定全等，只有满足C中的边、角对应相等时，可以由“ASA”判定两三角形全等.故选C. 在两个三角形中给出条件：①两角一边对应相等；②两边一角对应相等；③两角夹边对应相等；④两边夹角对应相等；⑤三边对应相等；⑥三角形对应相等．其中能判断出三角形全等的是( )
A. ①②③⑤ B. ①③④⑤
C. ①④⑤⑥ D. ②③④⑤
B
【解析】试题解析：①正确，符合AAS；
②不正确，该角应该是两边的夹角；
③正确，符合ASA；
④正确，符合SAS；
⑤正确，符合SSS；
⑥不正确，判定三角形全等必须有边的参与.
故选B. 如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）
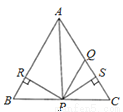
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
B
【解析】∵PR=PS，PR⊥AB于R，PS⊥AC于S，
∴∠PAB=∠PAC，∠PSA=∠PRA=90°，
在△PAR和△PAS中，
，
∴△PAR≌△PAS（AAS），
∴AR=AS，∴①正确；
∵AQ=PQ，
∠CAP=∠APQ，
∵∠CAP=∠BAP，
∴∠BAP=∠APQ，
∴PQ∥AB，∴②正确；
∵PR⊥AB，... 已知四条线段的长分别为2、3、4、5，用其中的三条线段构成的三角形的周长是_____________.
9或11或12
【解析】试题解析：由四条线段组成三角形的情况有：2，3，4；2，4，5；3，4，5，
故周长为9或11或12.
故答案为：9或11或12. 如图，在△ABC中，点P是△ABC三条角平分线的交点，则∠PBC＋∠PCA＋∠PAB=___度．
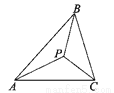
90
【解析】试题分析：由在△ABC中，点P是△ABC的内心，根据三角形的内心是三角形三条角平分线的交点，即可得∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，又由三角形内角和定理，即可求得∠PBC+∠PCA+∠PAB的度数．
试题解析：∵在△ABC中，点P是△ABC的内心，
∴∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，
∵∠ABC+∠BCA+... 如图，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是_________
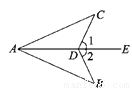
∠B=∠C等
【解析】试题解析：需添加的一个条件是：∠B=∠C，
理由：∵∠1=∠2，
∴∠ADC=∠ADB，
在△ABD和△ACD中，
∴△ABD≌△ACD(AAS).
故答案为：∠B=∠C.(答案不唯一). 如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D.给出下列结论：①∠EAB=∠FAC；②AF=AC；③∠C=∠EFA；④AD=AC.其中正确的结论是_____(填序号)．
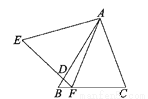
①②③
【解析】【解析】
在△AEF和△ABC中，∵AB=AE，∠B=∠E，BC=EF，∴△AEF≌△ABC（SAS），∴∠EAF=∠BAC，AF=AC，∠C=∠EFA，∴∠EAB=∠FAC，故①②③正确，④错误；
所以答案为：①②③． 如图，在△ABD和△ACE中，有下列四个判断：①AB=AC；②AD=AE；③∠B=∠C；④BD=CE，请以其中三个判断为条件，另一个为结果，写出一个正确的结论______________________(用序号???⇒?形式写出)．
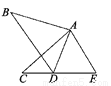
①②④⇒③或①③④⇒②
【解析】试题解析：由①②④⇒③或①③④⇒②；
先证前一种：
∵AB=AC，AD=AE，BD=CE，
∴△ABD≌△ACE(SSS)；
∴∠B=∠C；
再证第二种：
∵AB=AC，∠B=∠C，BD=CE，
∴△ABD≌△ACE(SAS)；
∴AD=AE.
故答案为：①②④⇒③或①③④⇒②；