题目内容
如图，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC交AD于点E，EF∥AC，下列结论一定成立的是( )
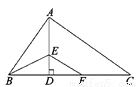
A. AB=BF B. AE=ED
C. AD=DC D. ∠ABE=∠DFE
A
【解析】【解析】
∵∠BAD+∠ABD=90°，∠ABD+∠C=90°
∴∠BAD=∠C（同角的余角相等）
又∵EF∥AC
∴∠BFE=∠C
∴∠BAD=∠BFE
又∵BE平分∠ABC
∴∠ABE=∠FBE
∴∠BEF=∠AEB，
在△ABE与△FBE中，
∠BEF=∠AEB，BE=BE，∠ABE=∠FBE
∴△ABE≌△FB...
练习册系列答案
相关题目
如图，点B、E、C、F在一条直线上，AB∥DE，AB=DE，BE=CF，AC=6，则DF=
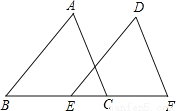
6.
【解析】
试题分析：根据题中条件由SAS可得△ABC≌△DEF，根据全等三角形的性质可得AC=DF=6．
试题解析: ∵AB∥DE，
∴∠B=∠DEF
∵BE=CF，
∴BC=EF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴AC=DF=6． 小华要设计一个摸球游戏,使得摸到红球的概率为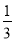
,如果设计符合要求,那么他周末就可以逛公园了,但妈妈对他的设计作出如下要求:(1)至少有四种颜色的球;
(2)至少有一个球是黄球.小华应该怎样设计呢?
答案见解析
【解析】试题分析：用6个球，其中2个红球，1个白球、1个蓝球，2个黄球，从而设计出摸球游戏．
试题解析：【解析】
用6个除颜色外完全相同的红球、白球、蓝球、黄球设计一个摸球游戏，其中2个红球，1个白球、1个蓝球，2个黄球． 在△ABC中，AB=AC=12cm，BC=6cm，D为BC的中点，动点P从B点出发，以每秒1cm的速度沿B→A→C的方向运动，设运动时间为t，那么当t=_________秒时，过D、P两点的直线将△ABC的周长分成两个部分，使其中一部分是另一部分的2倍．
7或17
【解析】试题解析：分两种情况：
（1）P点在AB上时，如图，
∵AB=AC=12cm，BD=CD=BC=×6=3cm，
设P点运动了t秒，则BP=t，AP=12-t，由题意得：
BP+BD=（AP+AC+CD）或（BP+BD）=AP+AC+CD，
∴t+3=（12-t+12+3）①或（t+3）=12-t+12+3②，
解①得t=7秒，解②得，t=... 已知四条线段的长分别为2、3、4、5，用其中的三条线段构成的三角形的周长是_____________.
9或11或12
【解析】试题解析：由四条线段组成三角形的情况有：2，3，4；2，4，5；3，4，5，
故周长为9或11或12.
故答案为：9或11或12. 若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A. 一种饮料重约300g，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
不少于1.5克
【解析】
试题分析：根据“蛋白质含量≥0.5%”，即可得到结果.
300×0.5%=1.5克
答：其中蛋白质的含量不少于1.5克. 用不等式表示图中的解集，其中正确的是( )
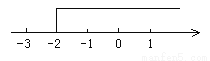
A. x≥－2 B. x＞－2 C. x＜－2 D. x≤－2
A
【解析】
试题分析：根据不等式的解集在数轴上表示出来的方法即可得到结果.
用不等式表示图中的解集为x≥－2，故选A. 如图，△ABC沿直线l向右移了3厘米，得△FDE，且BC＝6厘米，∠B＝40°.
(1)求BE；
(2)求∠FDB的度数；
(3)找出图中相等的线段(不另添加线段)；
(4)找出图中互相平行的线段(不另添加线段)．
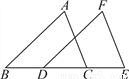
(1) 9厘米；(2) 140°；(3) AB＝FD、AC＝FE、BC＝DE、BD＝CE；(4) AB∥FD、AC∥FE.
【解析】试题分析：（1）根据平移的性质可得CE＝3cm，然后根据BE＝BC＋CE即可得出结论；
（2）根据平移的性质得出∠FDE的度数，然后根据邻补角互补即可得出答案；
（3）直接根据平移的性质即可得出结论；
（4）根据平移的性质即可得出结论．
...