题目内容
如图，在△ABD和△ACE中，有下列四个判断：①AB=AC；②AD=AE；③∠B=∠C；④BD=CE，请以其中三个判断为条件，另一个为结果，写出一个正确的结论______________________(用序号???⇒?形式写出)．
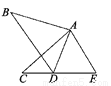
①②④⇒③或①③④⇒②
【解析】试题解析：由①②④⇒③或①③④⇒②；
先证前一种：
∵AB=AC，AD=AE，BD=CE，
∴△ABD≌△ACE(SSS)；
∴∠B=∠C；
再证第二种：
∵AB=AC，∠B=∠C，BD=CE，
∴△ABD≌△ACE(SAS)；
∴AD=AE.
故答案为：①②④⇒③或①③④⇒②；
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为 .
72
【解析】由AB=AC，CD平分∠ACB，∠A=36°，根据三角形内角和180°可求得∠B等于∠ACB，并能求出其角度，在△DBC求得所求角度．
【解析】
∵AB=AC，CD平分∠ACB，∠A=36°，
∴∠B=（180°-36°）÷2=72°，∠DCB=36°．
∴∠BDC=72°．
故答案为：72° 用力转动如图所示的转盘甲和转盘乙的指针,如果想让指针停在阴影区域,选取哪个转盘成功的机会比较大?( )
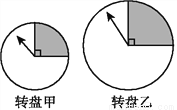
A. 转盘甲 B. 转盘乙 C. 两个一样大 D. 无法确定
C
【解析】【解析】
虽然两圆面积不同，但是阴影部分均占，故指针指向黑色部分的概率相同．故选C． 甲、乙两人玩扑克牌游戏,他们准备了13张从A到K的牌,并规定甲抽到7至K的牌,算甲胜,若抽到的是7以下的牌,则算乙胜,这种游戏对甲、乙来说___________.(填“公平”或“不公平”)
不公平
【解析】【解析】
P（甲胜）=，P（乙胜）=，故这种游戏对甲、乙来说不公平．故答案为：不公平． 如图，AD⊥BD，AE平分∠BAC，∠B=30°，∠ACD=70°.求∠DAE的度数．
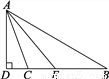
40°.
【解析】试题分析：根据三角形的内角和求出根据∠ACD=70°，求出的度数，求出根据角平分线的性质求出
即可求解.
试题解析：
∵AE平分∠BAC， 如图所示，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列三个结论：①AS=AR；②QP∥AR；③△BPR≌△QPS中（ ）
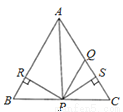
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
B
【解析】∵PR=PS，PR⊥AB于R，PS⊥AC于S，
∴∠PAB=∠PAC，∠PSA=∠PRA=90°，
在△PAR和△PAS中，
，
∴△PAR≌△PAS（AAS），
∴AR=AS，∴①正确；
∵AQ=PQ，
∠CAP=∠APQ，
∵∠CAP=∠BAP，
∴∠BAP=∠APQ，
∴PQ∥AB，∴②正确；
∵PR⊥AB，... 不一定在三角形内部的线段是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
C
【解析】试题解析：三角形的角平分线、中线一定在三角形的内部，
直角三角形的高线有两条是三角形的直角边，
钝角三角形的高线有两条在三角形的外部，
所以，不一定在三角形内部的线段是三角形的高.
故选C. 不等式－5x≥－13的解集中，最大的整数解是__________．
x＝2．
【解析】 解得： ，故最大的整数解为x=2.故答案为x=2. 下列图形中，∠1与∠2是对顶角的是( )
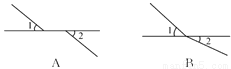
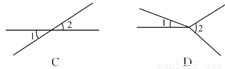
A. （A） B. （B） C. （C） D. （D）
C
【解析】由对顶角的定义：“有公共顶点，且两边分别互为反向延长线的两个角互为对顶角”分析可知，A、B、D三幅图中的∠1、∠2都不是对顶角，只有C图中的∠1、∠2是对顶角.
故选C.