题目内容
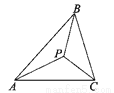
如图，在△ABC中，点P是△ABC三条角平分线的交点，则∠PBC＋∠PCA＋∠PAB=___度．
90
【解析】试题分析：由在△ABC中，点P是△ABC的内心，根据三角形的内心是三角形三条角平分线的交点，即可得∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，又由三角形内角和定理，即可求得∠PBC+∠PCA+∠PAB的度数．
试题解析：∵在△ABC中，点P是△ABC的内心，
∴∠PBC=∠ABC，∠PCA=∠ACB，∠PAB=∠BAC，
∵∠ABC+∠BCA+...
快乐小博士巩固与提高系列答案如图，在△ABC中，AB＝AC，∠ABC＝75°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为( )
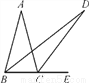
A. 15° B. 17.5° C. 20° D. 22.5°
A
【解析】因为AB＝AC，∠ABC＝75°，所以∠A=30°.
因为∠ABC与∠ACE的平分线相交于点D，所以∠ABD=∠EBD，∠ACD=∠ECD.
设ABD=∠EBD=x，∠ACD=∠ECD=y，则
2y=2x+30°①，
y=x+∠D ②
联立①②得，∠D=15°.
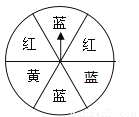
故选A. 如图，转盘中6个小扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向红色区域的概率为 ．
．
【解析】
试题分析：∵圆被等分成6份，其中红色部分占2份，∴落在阴影区域的概率==，故答案为：． 如图所示，已知B、E分别是线段AC、DF的中点，AC=DF，BF交CD于点H，AE交CD于点G，CH=HG=DG，BH=GE.
(1)填空：因为B、E分别是线段AC、DF的中点，所以CB=________AC，DE=________DF.因为AC=DF，所以CB=________.在△CBH和△DEG中，因为CB=________，CH=________，BH=________EG，所以________≌________(SSS)．
(2)除了(1)中的全等三角形外，请你再写出另外一对全等三角形，并说明理由．
(1) ， ，DE，DE，DG，△CBH，△DEG. （2）证明见解析.
【解析】试题分析：（1）因为B是AC的中点， 同理因为AC=DF，由上知根据上面求得： 即可得△CBH≌△DEG.两个三角形对应的三边相等，则两个三角形全等，所以找出三角形对应的三边
（2）根据题中条件分析，再用SAS来证明即可
试题解析：（1）因为B是AC的中点， 同理
因为AC=DF，由上知根据上... 如图，A、B、C分别是线段A1B、B1C、C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积为____.
7
【解析】试题分析：如下图，连接A1C，B1A，C1B，，因B是线段B1C的中点，所以B1B="BC." △A1B1A和△AB1B等底同高，根据等底同高的两个三角形面积相等可得S△B1AB=S△ABC=1；同理可得S△A1B1A=S△AB1B=1；所以=S△A1B1A+S△AB1B=1+1=2；同理可得S△C1CB1=2， S△C1AA1=2.
S△A1B1C1= S△A1BB1+ ... 如图，在△ABC中，CD是AB边上的高，BE是AC边的高，点O是两条高的交点，则∠A与∠1＋∠2的大小关系是( )
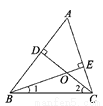
A. ∠A＞∠1＋∠2 B. ∠A=∠1＋∠2
C. ∠A＜∠1＋∠2 D. 无法确定
B
【解析】试题解析：∵CD是AB边上的高，BE是AC边上的高，
∴∠OEC=∠ADC=
又∴△ACD和△OCE中，∠ACD=∠OCE，
∴∠A=∠EOC
又∵∠EOC=∠1+∠2，
∴∠A=∠1+∠2.
故选B. 一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
白球有9个，红球有14个．
【解析】【试题分析】设白球有x个，红球有y个，根据“白球的个数比红球少，但白球的2倍比红球多”，得 ，解得7.5＜x＜12，则x可以取8,9,10,11.
由于2x=60－3y=3（20－y） 得2x应是3的倍数，则x只能取9，y = = 14
即白球有9个，红球有14个．
【试题解析】
设白球有x个，红球有y个，由题意，得
由第一个... 若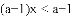
A. a＞0 B. a＜0 C. a＜1 D. a＞1
C
【解析】试题分析：根据不等式的基本性质即可得到关于a的不等式，解出即可.
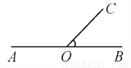
由题意得a-1＜0，a＜1，故选C. 如图，点Ａ，Ｏ，Ｂ在同一直线上，已知∠BOC=50°，则∠AOC=__________.
130°
【解析】因为∠BOC=50°,所以∠AOC=180°－∠BOC=180°－50°=130°,故答案为:130°.