题目内容
如图，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是_________
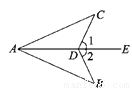
∠B=∠C等
【解析】试题解析：需添加的一个条件是：∠B=∠C，
理由：∵∠1=∠2，
∴∠ADC=∠ADB，
在△ABD和△ACD中，
∴△ABD≌△ACD(AAS).
故答案为：∠B=∠C.(答案不唯一).
期末1卷素质教育评估卷系列答案如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ）
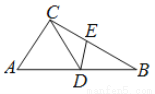
A. 50° B. 51° C. 51.5° D. 52.5°
D
【解析】试题分析：根据等腰三角形的性质推出∠A=∠CDA=50°，∠B=∠DCB，∠BDE=∠BED，根据三角形的外角性质求出∠B=25°，由三角形的内角和定理求出∠BDE=∠BED=（180°﹣25°）=77.5°，，根据平角的定义即可求出∠CDE=180°﹣∠CDA﹣∠EDB=180°﹣50°﹣77.5°=52.5°，故答案选D． 如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为_____．
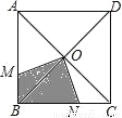
【解析】试题分析：∵四边形ABCD为正方形，点O是对角线的交点，
∴∠MBO=∠NCO=45°，OB=OC，∠BOC=90°，
∵∠MON=90°，
∴∠MOB+∠BON=90°，∠BON+∠NOC=90°，
∴∠MOB=∠NOC．
在△MOB和△NOC中，有，
∴△MOB≌△NOC（ASA）．
同理可得：△AOM≌△BON．
∴S阴影=S△BOC=... 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
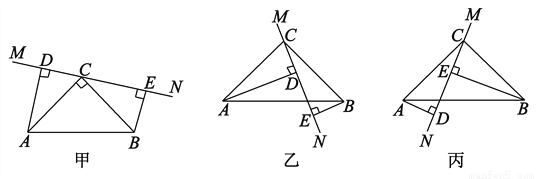
(1)当直线MN绕点C旋转到图甲的位置时，试说明：①△ADC≌△CEB；②DE=AD＋BE；
(2)当直线MN绕点C旋转到图乙的位置时，试说明：DE=AD－BE；
(3)当直线MN绕点C旋转到图丙的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
（1）证明见解析；（）证明见解析；（3）AD、DE、BE所满足的等量关系是DE=BE－AD(或AD=BE－DE，BE=AD＋DE等)理由见解析.
【解析】试题分析：（1）由∠ACB=90°，得∠BCE＋∠ACD=90°，而AD⊥MN于D，BE⊥MN于E.则∠ADC=∠CEB=90°，根据等角的余角相等得到∠ACD=∠CBE.，易得
Rt△ADC≌Rt△CEB，所以AD=CE，DC=BE... 在△ABC中，AB=AC=12cm，BC=6cm，D为BC的中点，动点P从B点出发，以每秒1cm的速度沿B→A→C的方向运动，设运动时间为t，那么当t=_________秒时，过D、P两点的直线将△ABC的周长分成两个部分，使其中一部分是另一部分的2倍．
7或17
【解析】试题解析：分两种情况：
（1）P点在AB上时，如图，
∵AB=AC=12cm，BD=CD=BC=×6=3cm，
设P点运动了t秒，则BP=t，AP=12-t，由题意得：
BP+BD=（AP+AC+CD）或（BP+BD）=AP+AC+CD，
∴t+3=（12-t+12+3）①或（t+3）=12-t+12+3②，
解①得t=7秒，解②得，t=... 根据下列已知条件，能画出唯一△ABC的是( )
A. AB=3，BC=4，CA=8 B. AB=4，BC=3，∠A=30°
C. ∠A=60°，∠B=45°，AB=4 D. ∠C=90°，AB=6
C
【解析】由一定的已知条件画三角形，要使画出的三角形是唯一的，说明不同的人根据这些条件画出的三角形一定是全等的；而由全等三角形的判定方法可知当两个三角形满足A、B、D选项中的边、角对应相等时，两个三角形不一定全等，只有满足C中的边、角对应相等时，可以由“ASA”判定两三角形全等.故选C. 若一个三角形的两边长分别为3和7，则第三边长可能是( )
A. 6 B. 3
C. 2 D. 11
A
【解析】试题解析：设第三条边长为x，根据三角形三边关系得：
7-3＜x＜7+3，
即4＜x＜10.
结合各选项数值可知，第三边长可能是6.
故选A. 不等式的解集在数轴上表示如图所示，则该不等式可能是___________________.
不唯一，如x－1≤0
【解析】由图形可知，不等式的解集为x≤1.只要所写的不等式的解集为x≤1，即可，答案不唯一. 如图，直线AB和CD相交于点O，则∠AOC的对顶角是__________.
∠BOD
【解析】因为AB和CD交于点O,则∠AOC的对顶角是∠BOC,故答案为:∠BOC.