题目内容
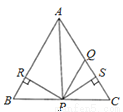
如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
 B
【解析】∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴∠PAB=∠PAC,∠PSA=∠PRA=90°,
在△PAR和△PAS中,
,
∴△PAR≌△PAS(AAS),
∴AR=AS,∴①正确;
∵AQ=PQ,
∠CAP=∠APQ,
∵∠CAP=∠BAP,
∴∠BAP=∠APQ,
∴PQ∥AB,∴②正确;
∵PR⊥AB,...
B
【解析】∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴∠PAB=∠PAC,∠PSA=∠PRA=90°,
在△PAR和△PAS中,
,
∴△PAR≌△PAS(AAS),
∴AR=AS,∴①正确;
∵AQ=PQ,
∠CAP=∠APQ,
∵∠CAP=∠BAP,
∴∠BAP=∠APQ,
∴PQ∥AB,∴②正确;
∵PR⊥AB,...
练习册系列答案
相关题目
如图,AB∥CE,BF交CE于点D,DE=DF,∠F=20°,则∠B的度数为______.

 40度
【解析】试题分析:由题可知,DE=DF,∠F=20°∴∠E=∠F=20°∴∠BDE=∠E+∠F=40°,又 AB∥CE,∴∠B=∠BDE=40°,故答案为40度。
40度
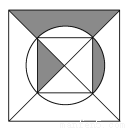
【解析】试题分析:由题可知,DE=DF,∠F=20°∴∠E=∠F=20°∴∠BDE=∠E+∠F=40°,又 AB∥CE,∴∠B=∠BDE=40°,故答案为40度。 在如图所示的正方形纸片上做随机扎针实验,则针头扎在阴影区域内的概率为( )
A.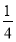 B.
B.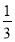
C.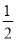 D.
D.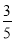
 A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为.
A
【解析】根据正方形的性质易证正方形的对角线把正方形分成的四个三角形均为同底等高的三角形,故其面积相等,故阴影部分的面积占一份,故针头扎在阴影区域的概率为. 如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.

 证明见解析.
【解析】试题分析:根据AB//CD得出∠DCA=∠CAB,结合AB=CE,AC=CD得出△CAB≌△DCE,从而得出答案.
试题解析:∵AB//CD,∴∠DCA=∠CAB 又∵AB=CE,AC=CD,∴△CAB≌△DCE ∴∠B=∠E.
证明见解析.
【解析】试题分析:根据AB//CD得出∠DCA=∠CAB,结合AB=CE,AC=CD得出△CAB≌△DCE,从而得出答案.
试题解析:∵AB//CD,∴∠DCA=∠CAB 又∵AB=CE,AC=CD,∴△CAB≌△DCE ∴∠B=∠E. 如图,在△ABD和△ACE中,有下列四个判断:①AB=AC;②AD=AE;③∠B=∠C;④BD=CE,请以其中三个判断为条件,另一个为结果,写出一个正确的结论______________________(用序号???⇒?形式写出).
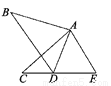
 ①②④⇒③或①③④⇒②
【解析】试题解析:由①②④⇒③或①③④⇒②;
先证前一种:
∵AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE(SSS);
∴∠B=∠C;
再证第二种:
∵AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE(SAS);
∴AD=AE.
故答案为:①②④⇒③或①③④⇒②;
①②④⇒③或①③④⇒②
【解析】试题解析:由①②④⇒③或①③④⇒②;
先证前一种:
∵AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE(SSS);
∴∠B=∠C;
再证第二种:
∵AB=AC,∠B=∠C,BD=CE,
∴△ABD≌△ACE(SAS);
∴AD=AE.
故答案为:①②④⇒③或①③④⇒②; 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )

A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙
 C
【解析】试题解析:由图形可知,甲有一边一角,不能判断两三角形全等,
乙有两边及其夹角,能判断两三角形全等,
丙得出两角及其一角对边,能判断两三角形全等,
根据全等三角形的判定得,乙丙正确.
故选C.
C
【解析】试题解析:由图形可知,甲有一边一角,不能判断两三角形全等,
乙有两边及其夹角,能判断两三角形全等,
丙得出两角及其一角对边,能判断两三角形全等,
根据全等三角形的判定得,乙丙正确.
故选C. |2a-24|+(3a-b-k)2=0,那么k取什么值时,b为负数.
 k大于36时b为负数.
【解析】【试题分析】根据绝对值和完全平方的非负性,得 解得:a=12,b=36-k,当b<0时,即36-k<0,解得k>36.
【试题解析】
由题意得: 解得:b=36-k,
解得k>36.
故答案为k>36.
k大于36时b为负数.
【解析】【试题分析】根据绝对值和完全平方的非负性,得 解得:a=12,b=36-k,当b<0时,即36-k<0,解得k>36.
【试题解析】
由题意得: 解得:b=36-k,
解得k>36.
故答案为k>36. 不等式2x<6的非负整数解为( )
A.0,1,2 B.1,2 C.0,-1,-2 D.无数个
 A
【解析】
试题分析:先根据不等式的基本性质求得不等式的解集,即可得到结果.
由2x<6得x<3,非负整数解为0,1,2
故选A.
A
【解析】
试题分析:先根据不等式的基本性质求得不等式的解集,即可得到结果.
由2x<6得x<3,非负整数解为0,1,2
故选A. 如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.
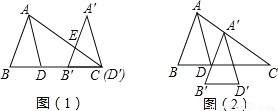
(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
 (1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=∠BAC,即可得出∠B′A′D′=∠B′A′C.
【解析】
(1)∠B′EC=...
(1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=∠BAC,即可得出∠B′A′D′=∠B′A′C.
【解析】
(1)∠B′EC=...