在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 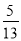 B.
B. 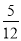 C.
C. 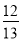 D.
D. 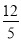
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 如果∠A为锐角,且sinA=0.6,那么( )
A. 0°<A<30° B. 30°<A<45°
C. 45°<A<60° D. 60°<A<90°
 B
【解析】∵sin30°="1/2," sin45°=,<0.6<
∴30°<∠A<45°,故选B
B
【解析】∵sin30°="1/2," sin45°=,<0.6<
∴30°<∠A<45°,故选B 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
 D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D.
D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D. 如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
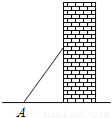
A. sinA的值越大,梯子越陡
B. cosA的值越大,梯子越陡
C. tanA的值越小,梯子越陡
D. 陡缓程度与∠A的函数值无关
 A
【解析】试题分析:锐角三角函数值的变化规律:正弦值和正切值都是随着角的增大而增大,余弦值和余切值都是随着角的增大而减小.
【解析】
根据锐角三角函数的变化规律,知sinA的值越大,∠A越大,梯子越陡.
故选:A.
A
【解析】试题分析:锐角三角函数值的变化规律:正弦值和正切值都是随着角的增大而增大,余弦值和余切值都是随着角的增大而减小.
【解析】
根据锐角三角函数的变化规律,知sinA的值越大,∠A越大,梯子越陡.
故选:A. sin70°,cos70°,tan70°的大小关系是( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
 D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D.
D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D. 随着锐角α的增大,cosα的值( )
A. 增大 B. 减小 C. 不变 D. 增大还是减小不确定
 B
【解析】随着锐角α的增大,cosα的值减小.
故选B.
B
【解析】随着锐角α的增大,cosα的值减小.
故选B. 当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是( )
A. 正弦和余弦 B. 正弦和正切 C. 余弦和正切 D. 正弦、余弦和正切
 B
【解析】当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是正弦和正切.
故选B.
B
【解析】当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是正弦和正切.
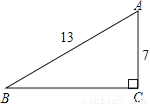
故选B. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
 .
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
.
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
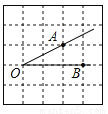
故答案为:. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于 .
 .
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
.
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.