题目内容
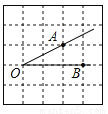
如图，将∠AOB放在边长为1的小正方形组成的网格中，则tan∠AOB= ．
．
【解析】试题分析：过点A作AD⊥OB垂足为D，如图，在直角△ABD中，AD=1，OD=2，则tan∠AOB==．故答案为： ．
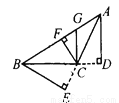
如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．
AD CF BE BFC FGC FAC GAC
【解析】试题解析：AD是△ABC中BC边上的高，是△ABC中AB边上的高，BE是△ABC中AC边上的高，CF是△ABC的高，也是△BFC、△FGC、△FAC、△GAC的高.
故答案是：AD、CF、BE、BFC、FGC、FAC、GAC. 剪纸是中国的民间艺术,剪纸的方法有很多,下面是一种剪纸的方法.如图,先将纸折叠,然后剪出图形,再展开,即可得到图案.
下面四个图案中,不能用上述方法剪出的是( )
A. 
B. 
C. 
D. 
C
【解析】将纸对折再对折将会出现两条互相垂直的折痕，剪出的图形是以这两条折痕为对称轴的轴对称图形，图A、图B、图D均能用上述方法剪出．图C是轴对称图形，但只有一条对称轴，所以将纸折叠不会剪出此图形．
故选：C. 已知sin6°=a，sin36°=b，则sin26°=（ ）
A. a2 B. 2a C. b2 D. b
A
【解析】∵sin6°=a，
∴=a2．
故选：A． 在Rt△ABC中，∠C=90°，CD是斜边AB上的高，如果CD=3，BD=2．求cos∠A的值.
【解析】分析：根据题意画出图形，进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可．
本题解析：
如图所示：
∵∠ACB=90°，∴∠B+∠A=90°，
∵CD⊥AB，∴∠CDA=90°，∴∠B+∠BCD=90°，∴∠BCD=∠A，
∵CD=3，BD=2，∴BC=
∴cosA=cos∠BCD=
故答案为： 如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）
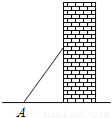
A. sinA的值越大，梯子越陡
B. cosA的值越大，梯子越陡
C. tanA的值越小，梯子越陡
D. 陡缓程度与∠A的函数值无关
A
【解析】试题分析：锐角三角函数值的变化规律：正弦值和正切值都是随着角的增大而增大，余弦值和余切值都是随着角的增大而减小．
【解析】
根据锐角三角函数的变化规律，知sinA的值越大，∠A越大，梯子越陡．
故选：A． 已知sin6°=a，sin36°=b，则sin26°=（ ）
A. a2 B. 2a C. b2 D. b
A
【解析】∵sin6°=a，
∴=a2．
故选：A． 如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请说明为何四边形AECF的面积为四边形ABCD的一半.
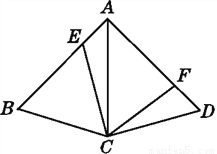
见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH，再利用面积间的等量代换即可推出结论.
证明：如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-... 如图所示，BA⊥CA，AB∥CD，AB＝CE，AC＝CD，则△ABC≌______，理由是_____，所以∠ABC＝______，∠ACB＝______，由此可知BC与DE的位置关系为__________.
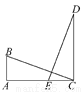
△CED SAS ∠CED ∠CDE 互相垂直
【解析】∵BA⊥CA，
∴∠BAC=90°，
∵AB∥CD，
∴∠ACD=∠BAC=90°，
在△ACB和△CDE中，
，
∴△ABC≌△ECD(SAS),
∴∠ABC＝∠CED，∠ACB＝∠CDE，
又因∠ACB+∠BCD=90°，
∴∠CDE+∠BCD=90°，
∴BC⊥DE.
...