题目内容
随着锐角α的增大,cosα的值( )
A. 增大 B. 减小 C. 不变 D. 增大还是减小不确定
 B
【解析】随着锐角α的增大,cosα的值减小.
故选B.
B
【解析】随着锐角α的增大,cosα的值减小.
故选B.
练习册系列答案
相关题目
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值.
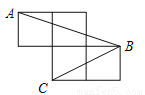
 ∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4...
∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4... 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )
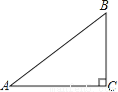
A. 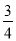 B.
B. 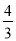 C.
C. 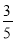 D.
D. 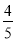
 C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A.
C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A. 比较下列三角函数值的大小:sin40°___________sin50°
 <
【解析】根据当0<α<90°,sinα随α的增大而增大即可得到:
∵40°<50°,
∴sin40°<sin50°.
故答案为<.
<
【解析】根据当0<α<90°,sinα随α的增大而增大即可得到:
∵40°<50°,
∴sin40°<sin50°.
故答案为<. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 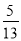 B.
B. 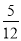 C.
C. 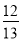 D.
D. 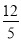
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. (3分)在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.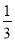 B.3 C.
B.3 C.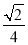 D.
D.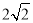
 D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D.
D.
【解析】
试题分析:设BC=x,则AB=3x,由勾股定理得,AC=,tanB===,故选D. 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
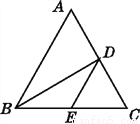
A. AD>DE B. AD=DE
C. AD<DE D. 不确定
 D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D.
D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=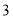 m,已知木箱高BE=
m,已知木箱高BE=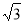 m,斜坡角为30°,则木箱端点E距地面AC的高度EF为 m.
m,斜坡角为30°,则木箱端点E距地面AC的高度EF为 m.
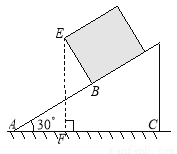
 3.
【解析】
试题分析:连接AE,在Rt△ABE中求出AE,根据∠EAB的正切值求出∠EAB的度数,继而得到∠EAF的度数,在Rt△EAF中,解出EF即可得出答案.
试题解析:连接AE,
在Rt△ABE中,AB=3m,BE=m,
则AE=m,
又∵tan∠EAB=,
∴∠EAB=30°,
在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,
...
3.
【解析】
试题分析:连接AE,在Rt△ABE中求出AE,根据∠EAB的正切值求出∠EAB的度数,继而得到∠EAF的度数,在Rt△EAF中,解出EF即可得出答案.
试题解析:连接AE,
在Rt△ABE中,AB=3m,BE=m,
则AE=m,
又∵tan∠EAB=,
∴∠EAB=30°,
在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,
... 
