题目内容
在Rt△ABC中，如果各边长度都扩大为原来的2倍，那么锐角A的正弦值（ ）
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
D
【解析】根据锐角三角函数的概念，知若各边长都扩大2倍，则sinA的值不变．
故选D．
练习册系列答案
名校课堂系列答案
相关题目
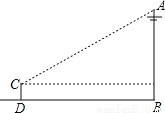
如图，为了测量电线杆AB的高度，小明将测量仪放在与电线杆的水平距离为9m的D处．若测角仪CD的高度为1.5m，在C处测得电线杆顶端A的仰角为36°，则电线杆AB的高度约为____（精确到0.1m）．（参考数据sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）．
8.1 m．
【解析】如图作CE⊥AB，垂足为E.
∵＝tan 36°，
CE＝BD，
∴AE＝BD·tan 36°
≈9×0.73
＝6.57，
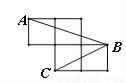
∴AB＝6.57＋1.5＝8.07≈8.1. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的正弦值为 ．
【解析】
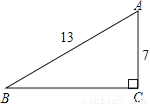
试题分析：本题首先将∠ABC转化到某一个直角三角形中，然后进行求值. 如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB= ．
．
【解析】试题分析：根据锐角三角函数定义直接进行解答．
【解析】
∵在Rt△ABC中，∠C=90°，AB=13，AC=7，
∴sinB==．
故答案为：． 在Rt△ABC中，各边的长度都扩大两倍，那么锐角A的各三角函数值（ ）
A．都扩大两倍 B．都缩小两倍 C．不变 D．都扩大四倍
C
【解析】
试题分析：根据三边对应成比例，两三角形相似，可知扩大后的三角形与原三角形相似，再根据相似三角形对应角相等解答．
【解析】
∵各边的长度都扩大两倍，
∴扩大后的三角形与Rt△ABC相似，
∴锐角A的各三角函数值都不变．
故选C． 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
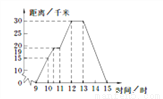
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
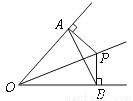
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 如图，OP平分∠AOB，PA⊥OA,PB⊥OB，垂足分别为A，B。下列结论中不一定成立的是（ ）
A、PA=PB B、PO平分∠AOB
C、OA=OB D、AB垂直平分OP
D
【解析】
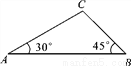
试题分析：本题要从已知条件OP平分∠AOB入手，利用角平分线的性质：因OP平分∠AOB，PA⊥OA，PB⊥OB，得到PA=PB，进而推出△AOE≌△BOE，从未得到∠APO=∠BPO，OA=OB，因此A、B、C项正确；设PO与AB相交于E，由OA=OB，∠AOP=∠BOP，OE=OE，得证△AOE≌△BOE，进而得∠AEO=∠BEO=90°，因此得证OP垂直AB，而不能得... 如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝2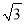
，则AB的长为_______．
3＋
【解析】过C作CD⊥AB于D，∴∠ADC＝∠BDC＝90°．∵∠B＝45°，∴∠BCD＝∠B＝45°，
∴CD＝BD．∵∠A＝30°，，∴，∴．
由勾股定理得： ，∴．