题目内容
在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于 .
 .
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
.
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
练习册系列答案
相关题目
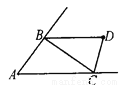
如图,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
 65°
【解析】试题解析:
故答案为:
65°
【解析】试题解析:
故答案为: 如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
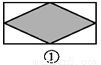
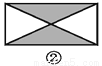
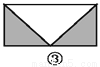
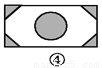
A. 4个 B. 3个 C. 2个 D. 1个
 A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A.
A
【解析】根据轴对称图形的概念即可判定.
【解析】
四副设计图中的阴影部分均为轴对称图形,故满足设计要求的图形有4个.
故选A. 如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
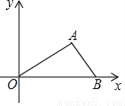
A. 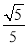 B.
B. 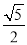 C.
C. 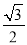 D.
D. 
 A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
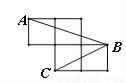
 【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值.
【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值. sin70°,cos70°,tan70°的大小关系是( )
A. tan70°<cos70°<sin70° B. cos70°<tan70°<sin70°
C. sin70°<cos70°<tan70° D. cos70°<sin70°<tan70°
 D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D.
D
【解析】根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.
又cos70°=sin20°,正弦值随着角的增大而增大,∴sin70°>cos70°=sin20°.
故选D. 在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B.都缩小两倍 C.不变 D.都扩大四倍
 C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C.
C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C. 如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.

 见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,...
见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,... 如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是________.
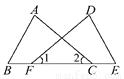
 AC=DF
【解析】已知∠1=∠2,BC=EF,根据“SAS”使△ABC≌△DEF,还需要补充的条件是AC=DF.
AC=DF
【解析】已知∠1=∠2,BC=EF,根据“SAS”使△ABC≌△DEF,还需要补充的条件是AC=DF.