题目内容
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
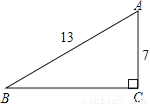
 .
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
.
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
练习册系列答案
相关题目
在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
 100°
【解析】试题解析:
①,
②,
①?②得, 解得
故答案为:
100°
【解析】试题解析:
①,
②,
①?②得, 解得
故答案为: 用一张正方形的红纸沿对角线对折后,得到一个等腰直角三角形,再沿斜边上的高对折,得到的又是等腰直角三角形,在此三角形上剪出一些花纹,然后打开折叠的纸,将它铺平,小明一下子就猜出了这个图案至少有( )条对称轴.
A. 0 B. 2 C. 4 D. 6
 B
【解析】根据轴对称的性质或动手操作即可得出答案.
【解析】
对折线有两条,而没展开的花纹不一定是轴对称,所以至少有2条对称轴.
故选B.
B
【解析】根据轴对称的性质或动手操作即可得出答案.
【解析】
对折线有两条,而没展开的花纹不一定是轴对称,所以至少有2条对称轴.
故选B. 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
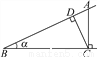
A. 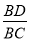 B.
B. 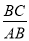 C.
C. 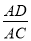 D.
D. 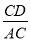
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C. 如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为 .
 【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以.
【解析】试题分析:因为在Rt△ABC中,∠C = 90°,AB = 2BC,所以. 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
 D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D.
D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D. 如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
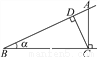
A. 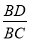 B.
B. 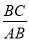 C.
C. 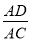 D.
D. 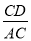
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C. 如图,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于点M,PN⊥CD于点N.
试说明:PM=PN.
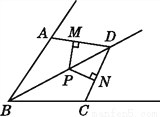
 见解析
【解析】根据角平分线的性质以及已知条件证得△ABD≌△CBD(SAS),然后由全等三角形的对应角相等推知∠ADB=∠CDB;再根据角平分线的判定定理即可得出结论.
证明:因为BD为∠ABC的平分线,
所以∠ABD=∠CBD.
又因为BA=BC,BD=BD,
所以△ABD≌△CBD(SAS).
所以∠ADB=∠CDB.
因为点P在BD上,PM⊥AD,...
见解析
【解析】根据角平分线的性质以及已知条件证得△ABD≌△CBD(SAS),然后由全等三角形的对应角相等推知∠ADB=∠CDB;再根据角平分线的判定定理即可得出结论.
证明:因为BD为∠ABC的平分线,
所以∠ABD=∠CBD.
又因为BA=BC,BD=BD,
所以△ABD≌△CBD(SAS).
所以∠ADB=∠CDB.
因为点P在BD上,PM⊥AD,... 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
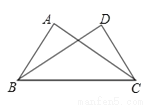
A. ∠A=∠D B. AB=DC C. ∠ACB=∠DBC D. AC=BD
 D
【解析】试题分析:根据题目所给条件∠ABC=∠DCB,再加上公共边BC=BC,然后再结合判定定理分别进行分析即可.
【解析】
A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
...
D
【解析】试题分析:根据题目所给条件∠ABC=∠DCB,再加上公共边BC=BC,然后再结合判定定理分别进行分析即可.
【解析】
A、添加∠A=∠D可利用AAS判定△ABC≌△DCB,故此选项不合题意;
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB,故此选项不合题意;
... 
