如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
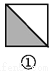
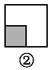
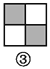
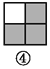
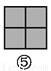
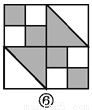
A. ①② B. ①③ C. ①④ D. ③⑤
 B
【解析】根据已知图形,利用分割与组合的原理对图形进行分析即可.
【解析】
如图所示:图案⑥是由图①和图③这两种基本图形拼接而成的.
故选:B.
B
【解析】根据已知图形,利用分割与组合的原理对图形进行分析即可.
【解析】
如图所示:图案⑥是由图①和图③这两种基本图形拼接而成的.
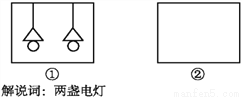
故选:B. 以给出的图形“○○,△△, ”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
 能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词:两人相伴.
能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
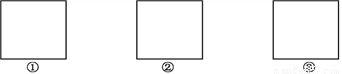
解说词:两人相伴. 将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
 答案不唯一,
【解析】分割后的整个图形必须是轴对称图形,作两边的中垂线;四块图形的完全相同,作法较多,符合要求即可.
【解析】
如图所示.
答案不唯一,
【解析】分割后的整个图形必须是轴对称图形,作两边的中垂线;四块图形的完全相同,作法较多,符合要求即可.
【解析】
如图所示. 观察图①~④中的左右两个图形,它们是否成轴对称?如果是,请画出其对称轴.

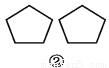
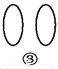
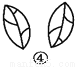
 见解析
【解析】判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合.若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
【解析】
图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称.
图①②③中成轴对称的两个图形的对称轴如图所示.
见解析
【解析】判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合.若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
【解析】
图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称.
图①②③中成轴对称的两个图形的对称轴如图所示. 下列图形是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】根据轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可..
【解析】
由轴对称图形的意义可知选项A中的图形是轴对称图形;而选项B、C、D中的图形均不是轴对称图形.
故选A.
A
【解析】根据轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可..
【解析】
由轴对称图形的意义可知选项A中的图形是轴对称图形;而选项B、C、D中的图形均不是轴对称图形.
故选A. 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
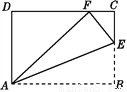
 32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
...
32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE,再利用等量代换即可求出四边形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为:
... 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )

A. 100° B. 80° C. 70° D. 50°
 A
【解析】试题分析:如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
【解析】
延长BD交AC于E.
∵DA=DB=DC,
...
A
【解析】试题分析:如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
【解析】
延长BD交AC于E.
∵DA=DB=DC,
... 如图,已知△ABC和△BDE均为等边三角形.试说明:BD+CD=AD.

 见解析
【解析】首先证明△ABE≌△CBD,进而得到DC=AE,再由AD=AE+ED利用等量代换即可证出AD=BD+CD.
证明:因为△ABC,△BDE均为等边三角形,
所以BE=BD=DE,AB=BC,∠ABC=∠EBD=60°.
所以∠ABE+∠EBC=∠DBC+∠EBC.
所以∠ABE=∠DBC.
在△ABE和△CBD中,
所以△ABE≌△CBD(S...
见解析
【解析】首先证明△ABE≌△CBD,进而得到DC=AE,再由AD=AE+ED利用等量代换即可证出AD=BD+CD.
证明:因为△ABC,△BDE均为等边三角形,
所以BE=BD=DE,AB=BC,∠ABC=∠EBD=60°.
所以∠ABE+∠EBC=∠DBC+∠EBC.
所以∠ABE=∠DBC.
在△ABE和△CBD中,
所以△ABE≌△CBD(S... 已知分式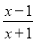 的值是零,那么x的值是( )
的值是零,那么x的值是( )
A. -1 B. 0
C. 1 D. ±1
 C
【解析】由题意得:x-1=0,则x=1,故选C.
C
【解析】由题意得:x-1=0,则x=1,故选C. 下列分式是最简分式的是( )
A. 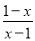 B.
B. 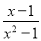
C. 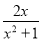 D.
D. 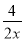
 C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.
C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.