题目内容
以给出的图形“○○,△△,
”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
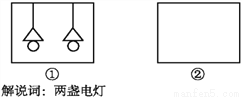
能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词：两人相伴.
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
在△ABC中，∠C＝90°，a＝5，c＝17，用科学计算器求∠A约等于 ( )
A. 17.6° B. 17°6′ C. 17°16′ D. 17.16°
A
【解析】试题解析：sinA=，
A=sin-10.294=17.6°，
故选A． 各边长均为整数且三边各不相等的三角形的周长小于13，这样的三角形个数共有( )
A. 5个 B. 4个 C. 3个 D. 2个
C
【解析】试题解析：根据三角形的两边之和大于第三边以及三角形的周长小于13，则其中的任何一边不能超过6.5；
再根据两边之差小于第三边，则这样的三角形共有3，4，2；4，5，2；3，4，5三个.
故选C. 某商场购进甲、乙两种商品，乙商品的单价是甲商品单价的2倍，若设甲商品的单价为x元，则购买240元甲商品的数量比购买300元乙商品的数量多____件．
【解析】设甲商品的单价为x元，乙商品的单价为2x元，根据购买240元甲商品的数量比购买300元乙商品的数量多．
故答案为： . 如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（ ）
A. 100° B. 80° C. 70° D. 50°
A
【解析】试题分析：如果延长BD交AC于E，由三角形的一个外角等于与它不相邻的两个内角的和，得∠BDC=∠DEC+∠ECD，∠DEC=∠ABE+∠BAE，所以∠BDC=∠ABE+∠BAE+∠ECD，又DA=DB=DC，根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°，∠ECD=∠DAC=30°，进而得出结果．
【解析】
延长BD交AC于E．
∵DA=DB=DC，
... 用一张正方形的红纸沿对角线对折后,得到一个等腰直角三角形,再沿斜边上的高对折,得到的又是等腰直角三角形,在此三角形上剪出一些花纹,然后打开折叠的纸,将它铺平,小明一下子就猜出了这个图案至少有( )条对称轴.
A. 0 B. 2 C. 4 D. 6
B
【解析】根据轴对称的性质或动手操作即可得出答案.
【解析】
对折线有两条，而没展开的花纹不一定是轴对称，所以至少有2条对称轴.
故选B. 在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，那么cos A的值等于 ．
．
【解析】
试题分析：∵在Rt△ABC中，∠C=90°，AC=4，BC=3，∴AB==，∴cosA==，故答案为：． 如图，在Rt△ABC中，∠C＝90°，AB＝2BC，则sinB的值为 .
【解析】试题分析：因为在Rt△ABC中，∠C = 90°，AB = 2BC，所以． 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
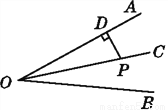
A. 6 B. 5 C. 4 D. 3
A
【解析】试题分析：如图，过点P作PE⊥OB于点E，∵OC是∠AOB的平分线，PD⊥OA于D，∴PE=PD，∵PD=6，∴PE=6，即点P到OB的距离是6．故选A．