题目内容
如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是( )

A. 100° B. 80° C. 70° D. 50°
 A
【解析】试题分析:如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
【解析】
延长BD交AC于E.
∵DA=DB=DC,
...
A
【解析】试题分析:如果延长BD交AC于E,由三角形的一个外角等于与它不相邻的两个内角的和,得∠BDC=∠DEC+∠ECD,∠DEC=∠ABE+∠BAE,所以∠BDC=∠ABE+∠BAE+∠ECD,又DA=DB=DC,根据等腰三角形等边对等角的性质得出∠ABE=∠DAB=20°,∠ECD=∠DAC=30°,进而得出结果.
【解析】
延长BD交AC于E.
∵DA=DB=DC,
...
练习册系列答案
相关题目
2013年4月20日雅安芦山县发生7.0级地震,某救援队赶赴灾区参加救援,救援队员现有一长为20m的梯子,为安全起见梯子靠在墙上的高度不能超过17.3m.求梯子与地面的夹角不超过___度时才是安全的.(精确到1°)
 59
【解析】试题解析:∵梯子靠住在墙上的高度不能超过17.3m,
∴梯子与地面的夹角最大为
∴∠A最大为
故答案为:
59
【解析】试题解析:∵梯子靠住在墙上的高度不能超过17.3m,
∴梯子与地面的夹角最大为
∴∠A最大为
故答案为: 化简: 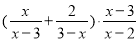 =____________.
=____________.
 1
【解析】根据分式的混合运算,先算括号里面的,再算乘法化简即可得===1.
故答案为:1.
1
【解析】根据分式的混合运算,先算括号里面的,再算乘法化简即可得===1.
故答案为:1. 下列运算正确的是( )
A. 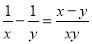 B.
B. 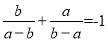
C. 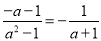 D.
D. 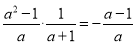
 B
【解析】根据分式的运算,可知:
A. =,故不正确;
B. =,故不正确;
C. =,故不正确;
D. =,故不正确.
故选:B.
B
【解析】根据分式的运算,可知:
A. =,故不正确;
B. =,故不正确;
C. =,故不正确;
D. =,故不正确.
故选:B. 以给出的图形“○○,△△, ”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
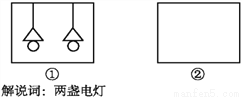
 能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词:两人相伴.
能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词:两人相伴. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,求∠ABC的正弦值.
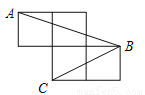
 ∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4...
∠ABC的正弦值为
【解析】试题分析:首先利用勾股定理计算出AB2,BC2,AC2,再根据勾股定理逆定理可证明∠BCA=90°,然后得到∠ABC的度数,再利用特殊角的三角函数可得∠ABC的正弦值.
试题解析:连接
AB2=32+12=10,BC2=22+12=5,AC=22+12=5,
∴AC=CB,BC2+AC2=AB2,
∴∠BCA=90°,
∴∠ABC=4... 如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值为( )
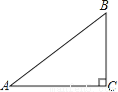
A. 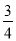 B.
B. 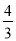 C.
C. 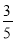 D.
D. 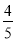
 C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A.
C
【解析】试题解析:在Rt△ABC中,∠C=90°,AC=3,BC=4,
由勾股定理,得
AB=.
cosA=,
故选A. 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
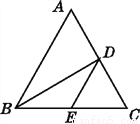
A. AD>DE B. AD=DE
C. AD<DE D. 不确定
 D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D.
D
【解析】根据角平分线上的点到角的两边距离相等可得点D到AB、BC的距离相等,AD、BE都不是点D到AB、BC的距离,大小不确定.
【解析】
∵BD平分∠ABC,
∴点D到AB、BC的距离相等,
∵AD不是点D到AB的距离,点E是BC上一点,
∴AD、DE的大小不确定.
故选D. 
