题目内容
如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
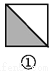
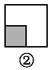
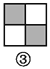
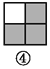
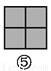
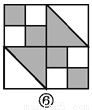
A. ①② B. ①③ C. ①④ D. ③⑤
B
【解析】根据已知图形，利用分割与组合的原理对图形进行分析即可．
【解析】
如图所示：图案⑥是由图①和图③这两种基本图形拼接而成的.
故选：B.
练习册系列答案
相关题目
用计算器比较大小，错误的是( )
A. sin15°＜sin35°＜sin55°＜sin75°
B. cos15°＞cos35°＞cos55°＞cos75°
C. tan15°＞tan35°＞tan55°＞tan75°
D. cos50°＜sin50°＜tan50°
C
【解析】试题解析：A.正弦值随着角度的增大而增大，故正确.
B. 余弦值随着角度的增大而减小，故正确.
C. 正切值随着角度的增大而增大，故错误.
D.正确.
故选C. 周长为P的三角形中，最长边m的取值范围是 ( )
A. 
B. 
C. 
D. 
A
【解析】试题解析：三边相等时,
三边不相等时,最长边
所以,
故选A. 下面是小明化简分式的过程，请仔细阅读，并解答所提出的问题．
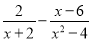
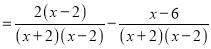第一步
＝2(x－2)－x＋6 第二步
＝2x－4－x＋6 第三步
＝x＋2 第四步
小明的解法从第___步开始出现错误，正确的化简结果是______．
二
【解析】根据分式的加减法，先对分式进行因式分解，然后通分为同分母的分式相加，再化简即可，因此错误在第二步，应为=.
故答案为：二、. 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
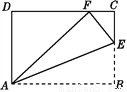
32(cm)
【解析】根据轴对称的性质可以得到AB=AF,BE=FE，再利用等量代换即可求出四边形纸片ABCD的周长.
解：由题意可知,△ABE和△AFE关于直线AE成轴对称,
所以AB=AF,BE=FE.
因为△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
所以四边形纸片ABCD的周长为：
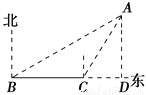
... 如图，已知灯塔A的周围7海里的范围内有暗礁，一艘渔轮在B处测得灯塔A在北偏东60°的方向，向正东航行8海里到C处后，又测得该灯塔在北偏东30°方向，渔轮不改变航向，继续向东航行，有没有触礁危险？请通过计算说明理由．(参考数据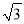
≈1.732)
有触礁危险，理由见解析.
【解析】试题分析：作AD⊥BC交BC的延长线于D，分别在Rt△ACD，Rt△ABD中求得CD、BD的长，再根据已知从而求得AD的值，然后与7进行比较，若大于7则无危险，否则有危险．
试题解析：作AD⊥BC交BC的延长线于D，
设AD=x,在Rt△ACD中,
在Rt△ABD中,
∵BC=8，
∵6.928海里<7海里，
∴有触礁危险... 如图，将∠AOB放在边长为1的小正方形组成的网格中，则tan∠AOB= ．
．
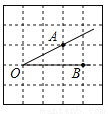
【解析】试题分析：过点A作AD⊥OB垂足为D，如图，在直角△ABD中，AD=1，OD=2，则tan∠AOB==．故答案为： ． 比较下列三角函数值的大小：sin40°______cos40°（选填“＞”、“=”、“＜”）
【解析】∵cos40°=sin50°，正弦值随着角的增大而增大，
又∵40°＜50°，
∴sin40°＜cos40° 根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
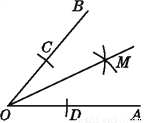
OM平分∠BOA
【解析】根据全等三角形的判定及性质即可得出结论.
【解析】
如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM.
又因为OM=OM,
所以△COM≌△DOM.
所以∠COM=∠DOM.
所以OM平分∠BOA.
故答案为：OM平分∠BOA.