△ABC中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，求∠A的度数．
44°
【解析】试题分析：先用∠A表示出∠C，再根据三角形的内角和等于180°列式整理用
∠A表示出∠B，再根据不等式求出∠A的取值范围，最后根据∠A是整数解答．
试题解析：
∵4∠C=7∠A，
∵∠A<∠B<∠C，
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍， 已知：如图，P是△ABC内任一点，求证：AB＋AC＞BP＋PC．
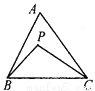
证明见解析.
【解析】试题分析：延长BP交AC于点D，由三角形的三边关系可得AB+AD＞BD，PD+DC＞PC，
试题解析：如图，延长BP交AC于点D.
在△ABD中，根据三边关系可得：
∵BD=BP+DP，
∴AB+AD＞BP+DP.
在△PCD中，根据三边关系可得：PD+DC＞PC， 如图，豫东有四个村庄A、B、C、D．现在要建造一个水塔P．请回答水塔P应建在何位置，才能使它到4村的距离之和最小，说明最节约材料的办法和理由．
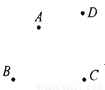
说明见解析.
【解析】试题分析：根据线段的性质：两点之间，线段距离最短；结合题意，要使它与四个村庄的距离之和最小，就要使它在AC与BD的交点处．
试题解析：
如图，水塔P应建在线段AC和线段BD的交点P处。这样的设计将最节省材料.
理由：我们不妨任意取一点P′,连接AP′、BP、CP′、DP′、AB、BC、CD、DA，
∵△AP′C中,AP′+CP′>AC=AP+CP... 已知a<0，则点P(-a2，-a+1)关于原点的对称点P′在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D
【解析】因为点P（-a2,-a+1）关于原点的对称点为P′,所以P′（a2,a-1）,
又因为a＜0,所以a-1＜0,a2＞0,所以P′在第四象限.故选D. 设点A与点B关于x轴对称，点A与点C关于y轴对称，则点B与点C( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称． D. 既关于x轴对称，又关于y轴对称
C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C. 将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )
A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)
D
【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D． 已知反比例函数和正比例函数在第一象限的交点为A（1，3），则在第三象限的交点B为（ ）
A. (-1，-3) B. (-3，-1) C. (-2，-6) D. (-6，-2)
A
【解析】因为反比例函数是中心对称图形,正比例函数与反比例函数的图象的两个交点关于原点对称,又因为一个交点的坐标为A（1,3）,所以它的另一个交点的坐标是（-1,-3）,故选A. 已知点A的坐标为（-2，3），点B的坐标为（0，1），则点A关于点B的坐标为（ ）
A. （ -2，2 ） B. （2，-3 ） C. （ 2，-1 ） D. （2，3 ）
C
【解析】因为点A的坐标为（-2,3）,点B的坐标为（0,1）,则点A关于点B的坐标为（2,-1）,故选C. 点P（x，y）关于x轴对称的点P1为______；关于y轴对称的点P2为______；关于原点的对称点P3为______.
（x，-y） （-x，y） （-x，-y）
【解析】点P（x,y）关于x轴对称的点P1为 （x，-y）,关于y轴对称的点P2为 （-x,y）,关于原点的对称点P3为（-x，-y）,故答案为:（x,-y）,（-x,y）,（-x,-y）. 已知点M的坐标为(3，-5)，则关于x轴对称的点的坐标点M’的坐标为___________，关于y轴对称的点M’的坐标为___________，关于原点对称的点的坐标为____________.
(3，5) (-3，-5) (-3，5)
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,所以点M（3, －5）关于x轴对称的点的坐标为（3, 5）,关于y轴对称点的坐标为（-3,-5）,关于原点对称的点的坐标为（-3,5）,故答案为: （3, 5）, （-3,-5）, （...