题目内容
设点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C( )
A. 关于x轴对称 B. 关于y轴对称 C. 关于原点对称. D. 既关于x轴对称,又关于y轴对称
 C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C.
C
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
点A与点B关于x轴对称,点A与点C关于y轴对称,则点B与点C原点对称,故选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图形不确定是轴对称图形的是( )
A. 角 B. 线段 C. 直线 D. 三角形
 D
【解析】【解析】
角、线段、直线都是轴对称图形;等腰三角形是轴对称图形,而一般的非等腰三角形不是轴对称图形.故选D.
D
【解析】【解析】
角、线段、直线都是轴对称图形;等腰三角形是轴对称图形,而一般的非等腰三角形不是轴对称图形.故选D. 下列各情景分别可以用哪一幅图来近似的刻画?正确的顺序是( )
①汽车紧急刹车(速度与时间的关系)
②人的身高变化(身高与年龄的关系)
③跳过运动员跳跃横杆(高度与时间的关系)
④一面冉冉上升的红旗(高度与时间的关系)

A.abcd B.dabc C.dbca D.cabd
 C
【解析】
试题分析:A、根据人的身高变化关系;
B、根据红旗高度与时间的关系;
C、跳过运动员跳跃横杆时高度与时间的关系;
D、汽车紧急刹车时速度与时间的关系.
【解析】
A、人的身高随着年龄的增加而增大,到一定年龄不变,故与②符合;
B、红旗升高随着时间的增加而增大,到一定时间不变,故与④符合;
C、运动员跳跃横杆时高度在上升到最大高度然后上...
C
【解析】
试题分析:A、根据人的身高变化关系;
B、根据红旗高度与时间的关系;
C、跳过运动员跳跃横杆时高度与时间的关系;
D、汽车紧急刹车时速度与时间的关系.
【解析】
A、人的身高随着年龄的增加而增大,到一定年龄不变,故与②符合;
B、红旗升高随着时间的增加而增大,到一定时间不变,故与④符合;
C、运动员跳跃横杆时高度在上升到最大高度然后上... 已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
 m=-3,n=-2.
【解析】试题分析:根据点关于原点对称的特征, 关于原点的对称点,横纵坐标都变成相反数,可得:2m+6=0,-3+1-n=0,解得: m=-3,n=-2.
试题解析:因为点A,B关于原点对称,所以,解得m=-3,n=-2.
m=-3,n=-2.
【解析】试题分析:根据点关于原点对称的特征, 关于原点的对称点,横纵坐标都变成相反数,可得:2m+6=0,-3+1-n=0,解得: m=-3,n=-2.
试题解析:因为点A,B关于原点对称,所以,解得m=-3,n=-2. 已知点M的坐标为(3,-5),则关于x轴对称的点的坐标点M’的坐标为___________,关于y轴对称的点M’的坐标为___________,关于原点对称的点的坐标为____________.
 (3,5) (-3,-5) (-3,5)
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,所以点M(3, -5)关于x轴对称的点的坐标为(3, 5),关于y轴对称点的坐标为(-3,-5),关于原点对称的点的坐标为(-3,5),故答案为: (3, 5), (-3,-5), (...
(3,5) (-3,-5) (-3,5)
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,所以点M(3, -5)关于x轴对称的点的坐标为(3, 5),关于y轴对称点的坐标为(-3,-5),关于原点对称的点的坐标为(-3,5),故答案为: (3, 5), (-3,-5), (... 已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
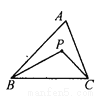
 说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A. 能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A. 中线 B. 角平分线 C. 高线 D. 三角形的角平分线
 A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A.
A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 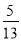 B.
B. 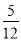 C.
C. 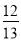 D.
D. 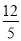
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 
